Question Number 151145 by mnjuly1970 last updated on 18/Aug/21

Answered by qaz last updated on 18/Aug/21
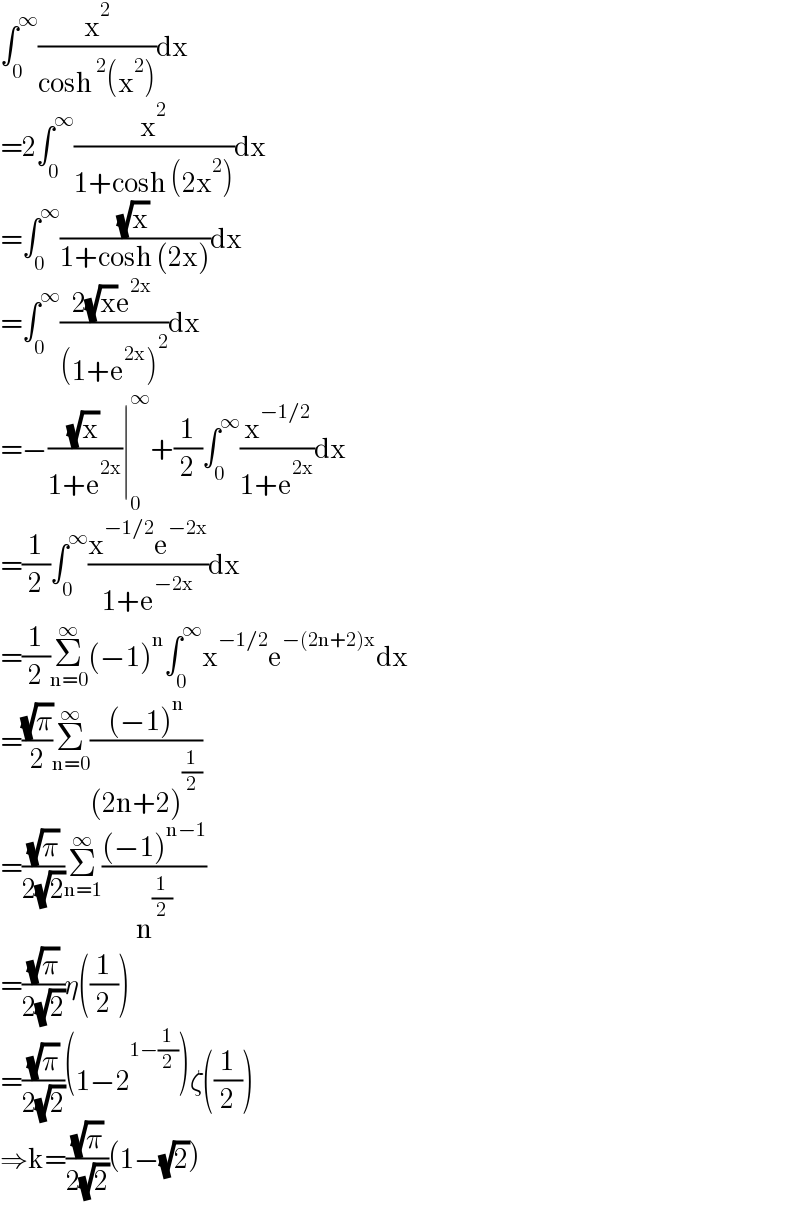
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{cosh}\:^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{cosh}\:\left(\mathrm{2x}^{\mathrm{2}} \right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{cosh}\:\left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}\sqrt{\mathrm{x}}\mathrm{e}^{\mathrm{2x}} }{\left(\mathrm{1}+\mathrm{e}^{\mathrm{2x}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=−\frac{\sqrt{\mathrm{x}}}{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\mid_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{−\mathrm{1}/\mathrm{2}} }{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{−\mathrm{1}/\mathrm{2}} \mathrm{e}^{−\mathrm{2x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\infty} \mathrm{x}^{−\mathrm{1}/\mathrm{2}} \mathrm{e}^{−\left(\mathrm{2n}+\mathrm{2}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\eta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \right)\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{k}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{1}−\sqrt{\mathrm{2}}\right) \\ $$
Commented by mnjuly1970 last updated on 18/Aug/21
$$\:\:{very}\:{nice}\:{mr}\:{qaz}… \\ $$
