Question Number 151162 by tabata last updated on 18/Aug/21
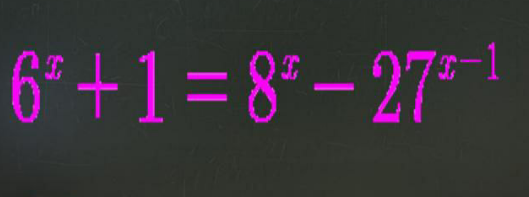
Commented by tabata last updated on 18/Aug/21

$${how}\:{can}\:{it}\:{solve} \\ $$
Commented by mr W last updated on 18/Aug/21
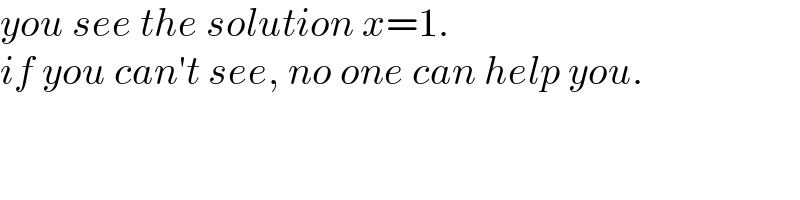
$${you}\:{see}\:{the}\:{solution}\:{x}=\mathrm{1}. \\ $$$${if}\:{you}\:{can}'{t}\:{see},\:{no}\:{one}\:{can}\:{help}\:{you}. \\ $$
Answered by Olaf_Thorendsen last updated on 18/Aug/21

$$\mathrm{6}^{{x}} +\mathrm{1}\:=\:\mathrm{8}^{{x}} −\mathrm{27}^{{x}−\mathrm{1}} \\ $$$$\bullet\:{x}\:=\:\mathrm{1}\:\mathrm{and}\:{x}\:=\:\mathrm{2}\:\mathrm{are}\:\mathrm{two}\:\mathrm{almost} \\ $$$$\mathrm{obvious}\:\mathrm{solutions}. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{have}\:: \\ $$$$\mathrm{2}^{{x}} \mathrm{3}^{{x}} +\mathrm{1}\:=\:\left(\mathrm{2}^{{x}} \right)^{\mathrm{3}} −\frac{\left(\mathrm{3}^{{x}} \right)^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\mathrm{Let}\:{a}\:=\:\mathrm{2}^{{x}} \:\mathrm{and}\:{b}\:=\:\mathrm{3}^{{x}} . \\ $$$${ab}+\mathrm{1}\:=\:{a}^{\mathrm{3}} −\frac{{b}^{\mathrm{3}} }{\mathrm{27}} \\ $$$${b}^{\mathrm{3}} +\mathrm{27}{ab}+\mathrm{27}−\mathrm{27}{a}^{\mathrm{3}} \:=\:\mathrm{0} \\ $$$$\left({b}^{\mathrm{3}} +{pb}+{q}\:=\:\mathrm{0}\right) \\ $$$$ \\ $$$$\mathrm{This}\:\mathrm{equation}\:\mathrm{may}\:\mathrm{be}\:\mathrm{viewed}\:\mathrm{as}\:\mathrm{a} \\ $$$$\mathrm{cubic}\:\mathrm{in}\:{b}.\: \\ $$$$ \\ $$$$\mathrm{Its}\:\mathrm{discriminant}\:\mathrm{is}\:: \\ $$$$\Delta_{{b}} \left({a}\right)\:=\:−\mathrm{4}{p}^{\mathrm{3}} −\mathrm{27}{q}^{\mathrm{2}} \\ $$$$\Delta_{{b}} \left({a}\right)\:=\:−\mathrm{4}\left(\mathrm{27}{a}\right)^{\mathrm{3}} −\mathrm{27}\left(\mathrm{27}−\mathrm{27}{a}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\Delta_{{b}} \left({a}\right)\:=\:−\mathrm{27}^{\mathrm{3}} \left(\mathrm{4}{a}^{\mathrm{3}} +\mathrm{1}−\mathrm{2}{a}^{\mathrm{3}} +{a}^{\mathrm{6}} \right) \\ $$$$\Delta_{{b}} \left({a}\right)\:=\:−\mathrm{27}^{\mathrm{3}} \left(\mathrm{1}+{a}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{wich}\:\mathrm{is}\:\mathrm{negative}\:\mathrm{for}\:\mathrm{all}\:\mathrm{a}\:\mathrm{except}\:\mathrm{for} \\ $$$${a}\:=\:−\mathrm{1},\:\mathrm{when}\:\mathrm{it}\:\mathrm{is}\:\mathrm{zero}.\:\mathrm{This}\:\mathrm{does}\:\mathrm{not}\: \\ $$$$\mathrm{correspond}\:\mathrm{to}\:\mathrm{a}\:\mathrm{real}\:\mathrm{value}\:\mathrm{of}\:{x},\:\mathrm{hence} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{values}\:\mathrm{of}\:{a}\:\mathrm{there}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{unique}\:\mathrm{real}\:{b}\:\mathrm{satisfying}\:\mathrm{the}\:\mathrm{polynomial} \\ $$$$\mathrm{which}\:\mathrm{is}\:: \\ $$$$ \\ $$$${b}\:=\:\mathrm{3}\left({a}−\mathrm{1}\right). \\ $$$$ \\ $$$$\mathrm{By}\:\mathrm{definition}\:\mathrm{we}\:\mathrm{have}\:{b}\:=\:\mathrm{3}^{\mathrm{log}_{\mathrm{2}} {a}} .\:\mathrm{So}\:\mathrm{it} \\ $$$$\mathrm{remains}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{3}^{\mathrm{log}_{\mathrm{2}} {a}} \:=\:\mathrm{3}\left({a}−\mathrm{1}\right). \\ $$$$\mathrm{By}\:\mathrm{inspection}\:\mathrm{we}\:\mathrm{find}\:\mathrm{the}\:\mathrm{solutions} \\ $$$${a}\:=\:\mathrm{2}\:\mathrm{and}\:{a}\:=\:\mathrm{4}\:\mathrm{corresponding}\:\mathrm{to}\:{x}\:=\:\mathrm{1} \\ $$$$\mathrm{and}\:{x}\:=\:\mathrm{2}.\:\mathrm{These}\:\mathrm{are}\:\mathrm{the}\:\mathrm{only}\:\mathrm{solutions}, \\ $$$$\mathrm{because}\:\mathrm{such}\:\mathrm{an}\:\mathrm{exponential}\:\mathrm{function} \\ $$$$\mathrm{intersects}\:\mathrm{any}\:\mathrm{line}\:\mathrm{in}\:\mathrm{at}\:\mathrm{most} \\ $$$$\mathrm{two}\:\mathrm{points}. \\ $$
