Question Number 151224 by mathdanisur last updated on 19/Aug/21
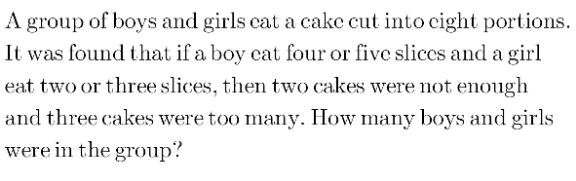
Answered by Rasheed.Sindhi last updated on 19/Aug/21
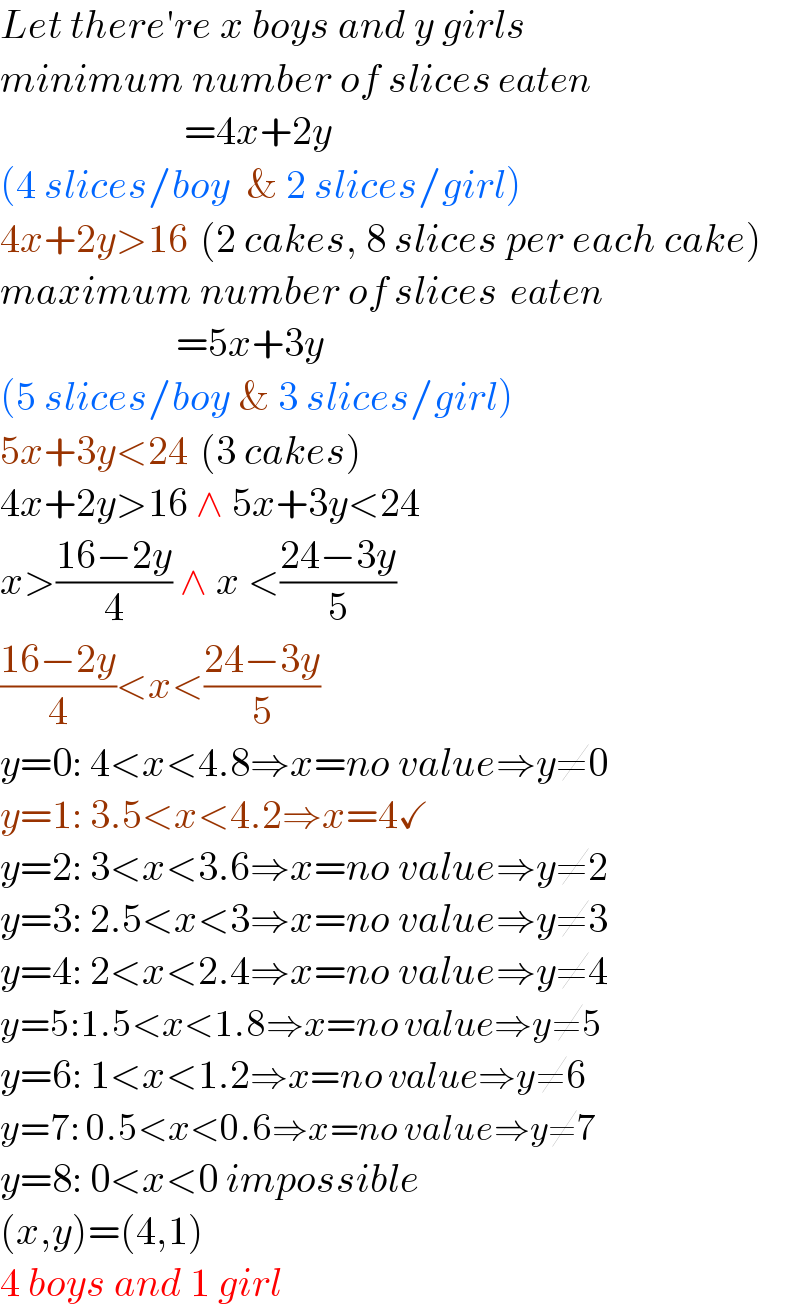
$${Let}\:{there}'{re}\:{x}\:{boys}\:{and}\:{y}\:{girls} \\ $$$${minimum}\:{number}\:{of}\:{slices}\:{eaten} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{x}+\mathrm{2}{y} \\ $$$$\left(\mathrm{4}\:{slices}/{boy}\:\:\&\:\mathrm{2}\:{slices}/{girl}\right) \\ $$$$\mathrm{4}{x}+\mathrm{2}{y}>\mathrm{16}\:\:\left(\mathrm{2}\:{cakes},\:\mathrm{8}\:{slices}\:{per}\:{each}\:{cake}\right) \\ $$$${maximum}\:{number}\:{of}\:{slices}\:\:{eaten} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}{x}+\mathrm{3}{y} \\ $$$$\left(\mathrm{5}\:{slices}/{boy}\:\&\:\mathrm{3}\:{slices}/{girl}\right) \\ $$$$\mathrm{5}{x}+\mathrm{3}{y}<\mathrm{24}\:\:\left(\mathrm{3}\:{cakes}\right) \\ $$$$\mathrm{4}{x}+\mathrm{2}{y}>\mathrm{16}\:\wedge\:\mathrm{5}{x}+\mathrm{3}{y}<\mathrm{24} \\ $$$${x}>\frac{\mathrm{16}−\mathrm{2}{y}}{\mathrm{4}}\:\wedge\:{x}\:<\frac{\mathrm{24}−\mathrm{3}{y}}{\mathrm{5}} \\ $$$$\frac{\mathrm{16}−\mathrm{2}{y}}{\mathrm{4}}<{x}<\frac{\mathrm{24}−\mathrm{3}{y}}{\mathrm{5}} \\ $$$${y}=\mathrm{0}:\:\mathrm{4}<{x}<\mathrm{4}.\mathrm{8}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{0} \\ $$$${y}=\mathrm{1}:\:\mathrm{3}.\mathrm{5}<{x}<\mathrm{4}.\mathrm{2}\Rightarrow{x}=\mathrm{4}\checkmark \\ $$$${y}=\mathrm{2}:\:\mathrm{3}<{x}<\mathrm{3}.\mathrm{6}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{2} \\ $$$${y}=\mathrm{3}:\:\mathrm{2}.\mathrm{5}<{x}<\mathrm{3}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{3} \\ $$$${y}=\mathrm{4}:\:\mathrm{2}<{x}<\mathrm{2}.\mathrm{4}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{4} \\ $$$${y}=\mathrm{5}:\mathrm{1}.\mathrm{5}<{x}<\mathrm{1}.\mathrm{8}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{5} \\ $$$${y}=\mathrm{6}:\:\mathrm{1}<{x}<\mathrm{1}.\mathrm{2}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{6} \\ $$$${y}=\mathrm{7}:\:\mathrm{0}.\mathrm{5}<{x}<\mathrm{0}.\mathrm{6}\Rightarrow{x}={no}\:{value}\Rightarrow{y}\neq\mathrm{7} \\ $$$${y}=\mathrm{8}:\:\mathrm{0}<{x}<\mathrm{0}\:{impossible} \\ $$$$\left({x},{y}\right)=\left(\mathrm{4},\mathrm{1}\right) \\ $$$$\mathrm{4}\:{boys}\:{and}\:\mathrm{1}\:{girl} \\ $$
Commented by mathdanisur last updated on 19/Aug/21
$$\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$
