Question Number 151350 by mathdanisur last updated on 20/Aug/21
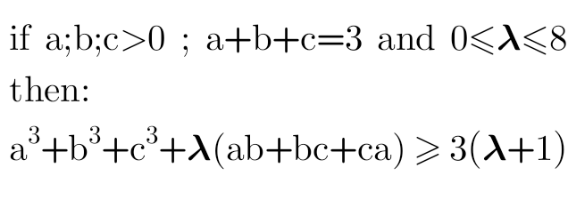
Commented by dumitrel last updated on 20/Aug/21
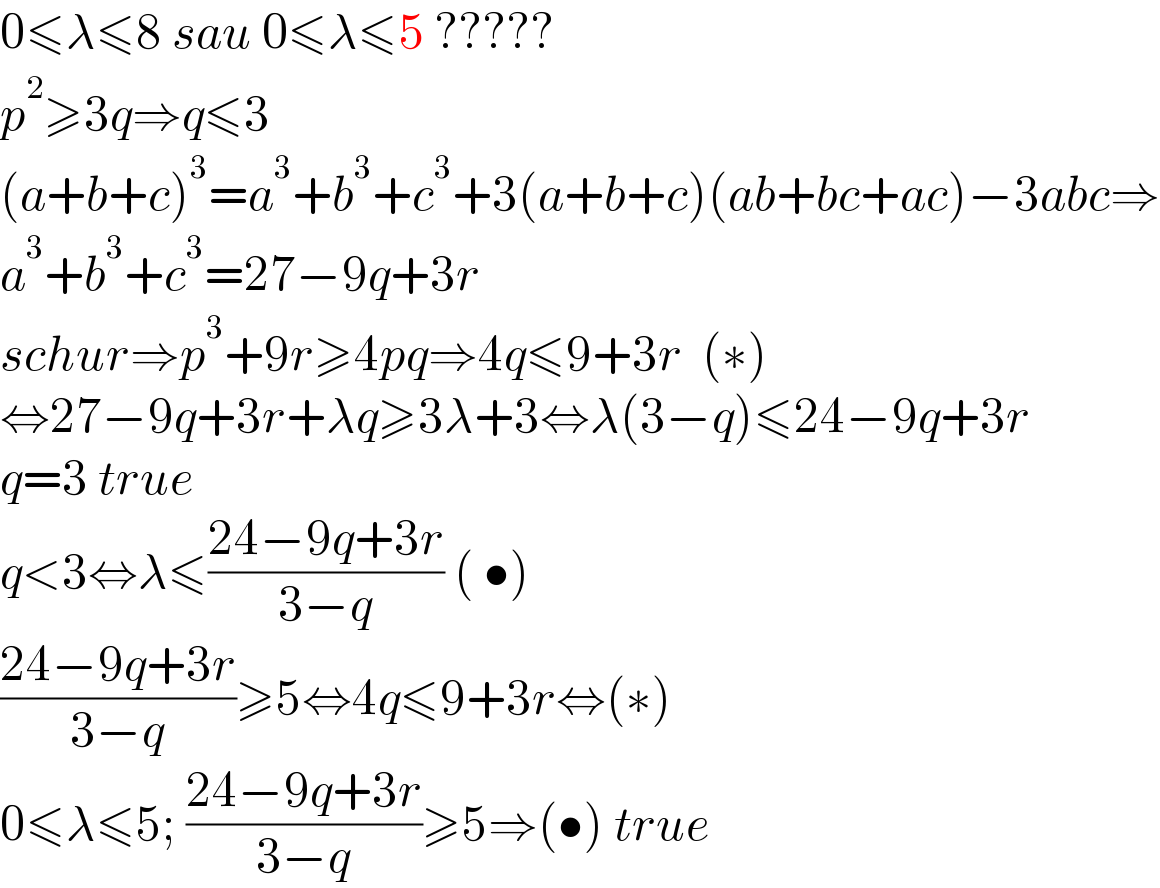
$$\mathrm{0}\leqslant\lambda\leqslant\mathrm{8}\:{sau}\:\mathrm{0}\leqslant\lambda\leqslant\mathrm{5}\:????? \\ $$$${p}^{\mathrm{2}} \geqslant\mathrm{3}{q}\Rightarrow{q}\leqslant\mathrm{3} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ac}\right)−\mathrm{3}{abc}\Rightarrow \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{27}−\mathrm{9}{q}+\mathrm{3}{r} \\ $$$${schur}\Rightarrow{p}^{\mathrm{3}} +\mathrm{9}{r}\geqslant\mathrm{4}{pq}\Rightarrow\mathrm{4}{q}\leqslant\mathrm{9}+\mathrm{3}{r}\:\:\left(\ast\right) \\ $$$$\Leftrightarrow\mathrm{27}−\mathrm{9}{q}+\mathrm{3}{r}+\lambda{q}\geqslant\mathrm{3}\lambda+\mathrm{3}\Leftrightarrow\lambda\left(\mathrm{3}−{q}\right)\leqslant\mathrm{24}−\mathrm{9}{q}+\mathrm{3}{r} \\ $$$${q}=\mathrm{3}\:{true} \\ $$$${q}<\mathrm{3}\Leftrightarrow\lambda\leqslant\frac{\mathrm{24}−\mathrm{9}{q}+\mathrm{3}{r}}{\mathrm{3}−{q}}\:\left(\:\bullet\right) \\ $$$$\frac{\mathrm{24}−\mathrm{9}{q}+\mathrm{3}{r}}{\mathrm{3}−{q}}\geqslant\mathrm{5}\Leftrightarrow\mathrm{4}{q}\leqslant\mathrm{9}+\mathrm{3}{r}\Leftrightarrow\left(\ast\right) \\ $$$$\mathrm{0}\leqslant\lambda\leqslant\mathrm{5};\:\frac{\mathrm{24}−\mathrm{9}{q}+\mathrm{3}{r}}{\mathrm{3}−{q}}\geqslant\mathrm{5}\Rightarrow\left(\bullet\right)\:{true} \\ $$
Commented by mathdanisur last updated on 20/Aug/21
$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{Cool} \\ $$
Commented by mathdanisur last updated on 20/Aug/21
$$\mathrm{true}\:\mathrm{Dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{0}\leqslant\lambda\leqslant\mathrm{5} \\ $$
Commented by dumitrel last updated on 20/Aug/21
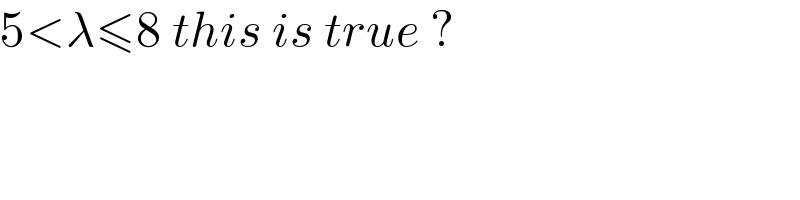
$$\mathrm{5}<\lambda\leqslant\mathrm{8}\:{this}\:{is}\:{true}\:? \\ $$
