Menu Close

Question-151393

Tinku Tara 0 Comments
Pin




Question Number 151393 by Tawa11 last updated on 20/Aug/21
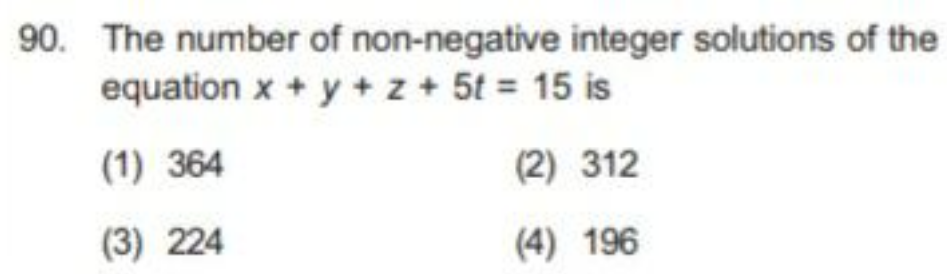
Answered by mr W last updated on 20/Aug/21
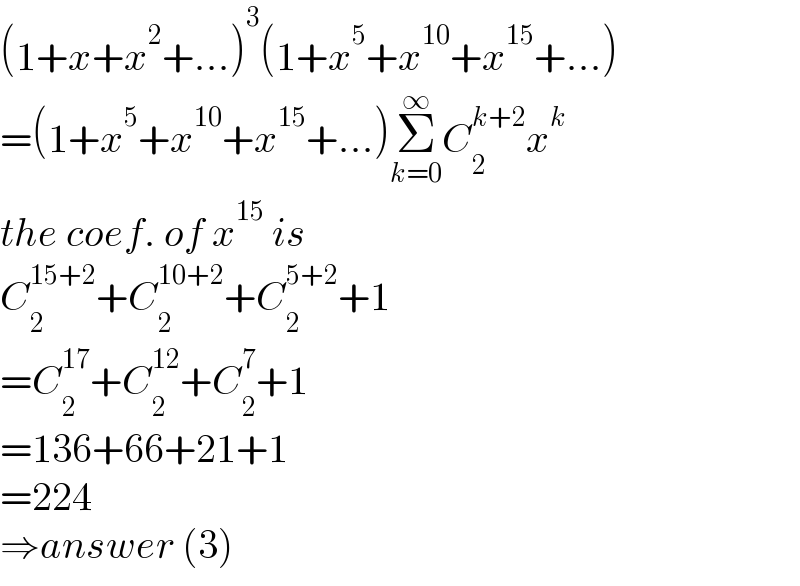
(1+x+x^2 +...)^3 (1+x^5 +x^(10) +x^(15) +...) =(1+x^5 +x^(10) +x^(15) +...)Σ_(k=0) ^∞ C_2 ^(k+2) x^k the coef. of x^(15) is C_2 ^(15+2) +C_2 ^(10+2) +C_2 ^(5+2) +1 =C_2 ^(17) +C_2 ^(12) +C_2 ^7 +1 =136+66+21+1 =224 ⇒answer (3)
$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{10}} +{x}^{\mathrm{15}} +…\right) \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{10}} +{x}^{\mathrm{15}} +…\right)\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}} \\ $$$${the}\:{coef}.\:{of}\:{x}^{\mathrm{15}} \:{is} \\ $$$${C}_{\mathrm{2}} ^{\mathrm{15}+\mathrm{2}} +{C}_{\mathrm{2}} ^{\mathrm{10}+\mathrm{2}} +{C}_{\mathrm{2}} ^{\mathrm{5}+\mathrm{2}} +\mathrm{1} \\ $$$$={C}_{\mathrm{2}} ^{\mathrm{17}} +{C}_{\mathrm{2}} ^{\mathrm{12}} +{C}_{\mathrm{2}} ^{\mathrm{7}} +\mathrm{1} \\ $$$$=\mathrm{136}+\mathrm{66}+\mathrm{21}+\mathrm{1} \\ $$$$=\mathrm{224} \\ $$$$\Rightarrow{answer}\:\left(\mathrm{3}\right) \\ $$
Commented by Tawa11 last updated on 20/Aug/21
Thanks sir. God bless you
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by mr W last updated on 20/Aug/21
an other not such smart way. find at first number of non−negative integer solution of x+y+z=n. x+y=n−z z=0 ⇒x+y=n ⇒n+1 solutions z=1 ⇒x+y=n−1 ⇒n solutions ... z=n ⇒x+y=0 ⇒ 1 solution totally 1+2+3+...+n+(n+1)=(((n+1)(n+2))/2) solutions x+y+z+5t=15 x+y+z=15−5t 1) t=0 ⇒x+y+z=15 ⇒(((15+1)(15+2))/2)=136 solutions 2) t=1 ⇒x+y+z=10 ⇒(((10+1)(10+2))/2)=66 solutions 3) t=2 ⇒x+y+z=5 ⇒(((5+1)(5+2))/2)=21 solutions 4) t=3 ⇒x+y+z=0 ⇒1 solution totally x+y+z+5t=15 has 136+66+21+1=224 solutions
$${an}\:{other}\:{not}\:{such}\:{smart}\:{way}. \\ $$$${find}\:{at}\:{first}\:{number}\:{of}\: \\ $$$${non}−{negative}\:{integer}\:{solution}\:{of}\: \\ $$$${x}+{y}+{z}={n}. \\ $$$${x}+{y}={n}−{z} \\ $$$${z}=\mathrm{0}\:\Rightarrow{x}+{y}={n}\:\Rightarrow{n}+\mathrm{1}\:{solutions} \\ $$$${z}=\mathrm{1}\:\Rightarrow{x}+{y}={n}−\mathrm{1}\:\Rightarrow{n}\:{solutions} \\ $$$$… \\ $$$${z}={n}\:\Rightarrow{x}+{y}=\mathrm{0}\:\Rightarrow\:\mathrm{1}\:{solution} \\ $$$${totally}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}+\left({n}+\mathrm{1}\right)=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{2}}\:{solutions} \\ $$$$ \\ $$$${x}+{y}+{z}+\mathrm{5}{t}=\mathrm{15} \\ $$$${x}+{y}+{z}=\mathrm{15}−\mathrm{5}{t} \\ $$$$\left.\mathrm{1}\right)\:{t}=\mathrm{0}\:\Rightarrow{x}+{y}+{z}=\mathrm{15} \\ $$$$\Rightarrow\frac{\left(\mathrm{15}+\mathrm{1}\right)\left(\mathrm{15}+\mathrm{2}\right)}{\mathrm{2}}=\mathrm{136}\:{solutions} \\ $$$$\left.\mathrm{2}\right)\:{t}=\mathrm{1}\:\Rightarrow{x}+{y}+{z}=\mathrm{10} \\ $$$$\Rightarrow\frac{\left(\mathrm{10}+\mathrm{1}\right)\left(\mathrm{10}+\mathrm{2}\right)}{\mathrm{2}}=\mathrm{66}\:{solutions} \\ $$$$\left.\mathrm{3}\right)\:{t}=\mathrm{2}\:\Rightarrow{x}+{y}+{z}=\mathrm{5} \\ $$$$\Rightarrow\frac{\left(\mathrm{5}+\mathrm{1}\right)\left(\mathrm{5}+\mathrm{2}\right)}{\mathrm{2}}=\mathrm{21}\:{solutions} \\ $$$$\left.\mathrm{4}\right)\:{t}=\mathrm{3}\:\Rightarrow{x}+{y}+{z}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\:{solution} \\ $$$${totally}\:{x}+{y}+{z}+\mathrm{5}{t}=\mathrm{15}\:{has} \\ $$$$\mathrm{136}+\mathrm{66}+\mathrm{21}+\mathrm{1}=\mathrm{224}\:{solutions} \\ $$
Commented by Tawa11 last updated on 20/Aug/21
Thanks for your time sir. I really appreciate. God bless you.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *