Question Number 151404 by saly last updated on 20/Aug/21
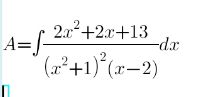
Commented by saly last updated on 20/Aug/21

$$\:\:\:\:\:\:{Do}\:{you}\:\:{help}\:{me}\:? \\ $$
Answered by MJS_new last updated on 20/Aug/21
![∫((2x^2 +2x+13)/((x^2 +1)^2 (x−2)))dx= =∫(dx/(x−2))−∫(x/(x^2 +1))dx−4∫(dx/(x^2 +1))+∫((2x^2 −3x−2)/((x^2 +1)^2 ))dx ∫(dx/(x−2))=ln ∣x−2∣ −∫(x/(x^2 +1))dx=−(1/2)∫((2x)/(x^2 +1))dx=−(1/2)ln (x^2 +1) −4∫(dx/(x^2 +1))=−4arctan x ∫((2x^2 −3x−2)/((x^2 +1)^2 ))dx=(((3/2)−2x)/(x^2 +1))=((3−4x)/(2(x^2 +1))) ((d/dx)[((ax+b)/(x^2 +1))]=((−ax^2 −2bx+a)/((x^2 +1)^2 )) ⇒ a=−2∧b=(3/2)) answer is ((3−4x)/(2(x^2 +1))) +(1/2)ln (((x−2)^2 )/(x^2 +1)) −4arctan x +C](https://www.tinkutara.com/question/Q151419.png)
$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{13}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)}{dx}= \\ $$$$=\int\frac{{dx}}{{x}−\mathrm{2}}−\int\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\mathrm{4}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}−\mathrm{2}}=\mathrm{ln}\:\mid{x}−\mathrm{2}\mid \\ $$$$−\int\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$−\mathrm{4}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}=−\mathrm{4arctan}\:{x} \\ $$$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{3}−\mathrm{4}{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\left(\frac{{d}}{{dx}}\left[\frac{{ax}+{b}}{{x}^{\mathrm{2}} +\mathrm{1}}\right]=\frac{−{ax}^{\mathrm{2}} −\mathrm{2}{bx}+{a}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:{a}=−\mathrm{2}\wedge{b}=\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\mathrm{answer}\:\mathrm{is} \\ $$$$\frac{\mathrm{3}−\mathrm{4}{x}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}\:−\mathrm{4arctan}\:{x}\:+{C} \\ $$
Commented by peter frank last updated on 21/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by saly last updated on 21/Aug/21

$$\:\:\:{thank}\:{you}! \\ $$
