Question Number 151435 by mathdanisur last updated on 21/Aug/21

Commented by peter frank last updated on 21/Aug/21
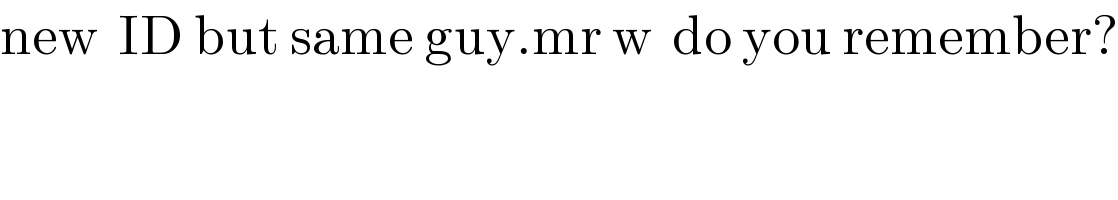
$$\mathrm{new}\:\:\mathrm{ID}\:\mathrm{but}\:\mathrm{same}\:\mathrm{guy}.\mathrm{mr}\:\mathrm{w}\:\:\mathrm{do}\:\mathrm{you}\:\mathrm{remember}? \\ $$
Commented by mr W last updated on 21/Aug/21
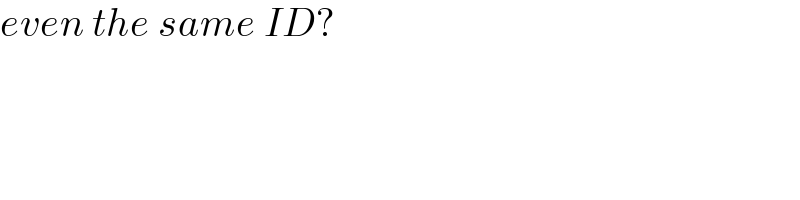
$${even}\:{the}\:{same}\:{ID}? \\ $$
Commented by peter frank last updated on 21/Aug/21

$$\mathrm{different}\:\mathrm{ID} \\ $$
Commented by Rasheed.Sindhi last updated on 24/Aug/21

$${Same}\:{or}\:{similar} \\ $$
Answered by mr W last updated on 21/Aug/21
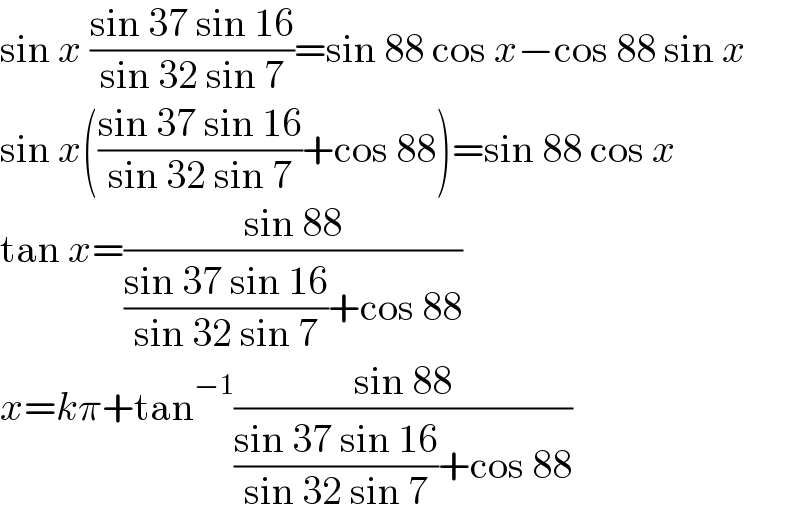
$$\mathrm{sin}\:{x}\:\frac{\mathrm{sin}\:\mathrm{37}\:\mathrm{sin}\:\mathrm{16}}{\mathrm{sin}\:\mathrm{32}\:\mathrm{sin}\:\mathrm{7}}=\mathrm{sin}\:\mathrm{88}\:\mathrm{cos}\:{x}−\mathrm{cos}\:\mathrm{88}\:\mathrm{sin}\:{x} \\ $$$$\mathrm{sin}\:{x}\left(\frac{\mathrm{sin}\:\mathrm{37}\:\mathrm{sin}\:\mathrm{16}}{\mathrm{sin}\:\mathrm{32}\:\mathrm{sin}\:\mathrm{7}}+\mathrm{cos}\:\mathrm{88}\right)=\mathrm{sin}\:\mathrm{88}\:\mathrm{cos}\:{x} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{sin}\:\mathrm{88}}{\frac{\mathrm{sin}\:\mathrm{37}\:\mathrm{sin}\:\mathrm{16}}{\mathrm{sin}\:\mathrm{32}\:\mathrm{sin}\:\mathrm{7}}+\mathrm{cos}\:\mathrm{88}} \\ $$$${x}={k}\pi+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{sin}\:\mathrm{88}}{\frac{\mathrm{sin}\:\mathrm{37}\:\mathrm{sin}\:\mathrm{16}}{\mathrm{sin}\:\mathrm{32}\:\mathrm{sin}\:\mathrm{7}}+\mathrm{cos}\:\mathrm{88}} \\ $$
Commented by mathdanisur last updated on 21/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by MJS_new last updated on 21/Aug/21
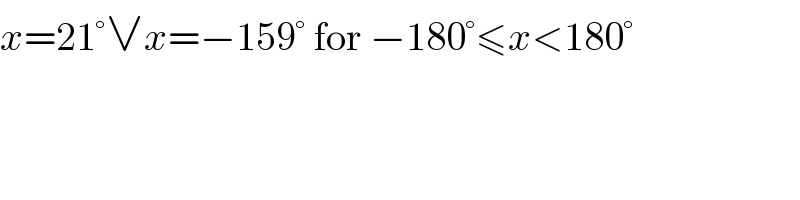
$${x}=\mathrm{21}°\vee{x}=−\mathrm{159}°\:\mathrm{for}\:−\mathrm{180}°\leqslant{x}<\mathrm{180}° \\ $$
