Question Number 151538 by DELETED last updated on 21/Aug/21

Answered by DELETED last updated on 21/Aug/21
![3). lim_(t→∞) [(sin (2/t))−(3/t)].(t/6)=..? =lim_(t→0) [(sin 2t)−3t].(1/(6t)) =lim_(t→0) [(((sin 2t)/(6t)))−(1/2)] =lim_(t→0) ((sin 2t)/(6t)) −lim_(t→0) (1/2) =(2/6)−(1/2)=(1/3)−(1/2)=((2−3)/6)=−(1/6)//](https://www.tinkutara.com/question/Q151542.png)
$$\left.\mathrm{3}\right).\:\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}}\:\left[\left(\mathrm{sin}\:\frac{\mathrm{2}}{\mathrm{t}}\right)−\frac{\mathrm{3}}{\mathrm{t}}\right].\frac{\mathrm{t}}{\mathrm{6}}=..? \\ $$$$\:\:\:\:\:\:=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\left(\mathrm{sin}\:\mathrm{2t}\right)−\mathrm{3t}\right].\frac{\mathrm{1}}{\mathrm{6t}} \\ $$$$\:\:\:\:\:\:=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\left(\frac{\mathrm{sin}\:\mathrm{2t}}{\mathrm{6t}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\right] \\ $$$$\:\:\:\:\:\:=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2t}}{\mathrm{6t}}\:−\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}−\mathrm{3}}{\mathrm{6}}=−\frac{\mathrm{1}}{\mathrm{6}}// \\ $$$$\:\:\:\:\:\: \\ $$$$ \\ $$
Answered by DELETED last updated on 21/Aug/21
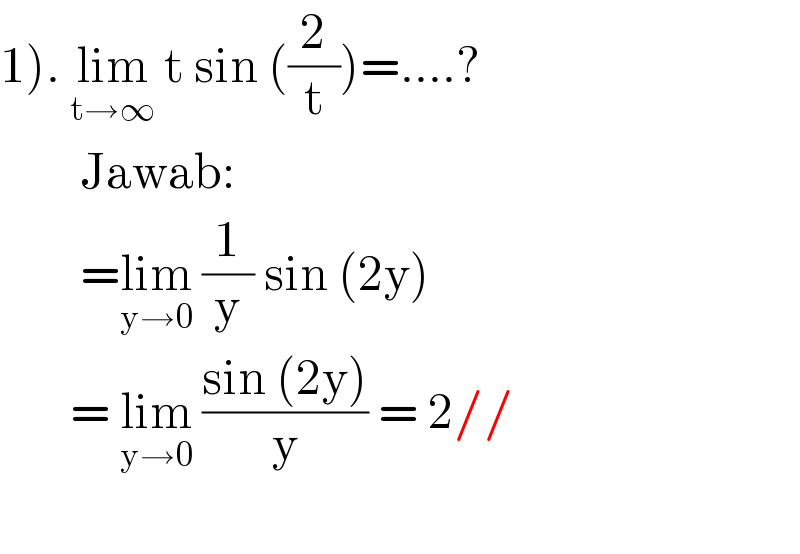
$$\left.\mathrm{1}\right).\:\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{t}\:\mathrm{sin}\:\left(\frac{\mathrm{2}}{\mathrm{t}}\right)=….? \\ $$$$\:\:\:\:\:\:\:\:\mathrm{Jawab}: \\ $$$$\:\:\:\:\:\:\:\:=\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{y}}\:\mathrm{sin}\:\left(\mathrm{2y}\right) \\ $$$$\:\:\:\:\:\:\:=\:\underset{\mathrm{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{2y}\right)}{\mathrm{y}}\:=\:\mathrm{2}// \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Answered by DELETED last updated on 21/Aug/21
![2). lim_( θ→∞ ) θ^2 (1−cos (2/θ) )=...? =lim_( θ→∞ ) θ^2 [1−(1−2sin^2 (1/θ) ] =lim_( θ→∞ ) θ^2 [2sin^2 (1/θ) ] =lim_(θ→0) ((1/θ^2 ))(2sin^2 θ) =2lim_(θ→0) (sin^2 θ) =2 lim_(θ→0) (((sin^2 θ))/θ^2 ) =2×1=2//](https://www.tinkutara.com/question/Q151541.png)
$$\left.\mathrm{2}\right).\:\underset{\:\theta\rightarrow\infty\:} {\mathrm{lim}}\:\theta^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\frac{\mathrm{2}}{\theta}\:\right)=…? \\ $$$$\:\:\:\:\:\:=\underset{\:\theta\rightarrow\infty\:} {\mathrm{lim}}\:\theta^{\mathrm{2}} \left[\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \:\frac{\mathrm{1}}{\theta}\:\right]\right. \\ $$$$\:\:\:\:\:\:=\underset{\:\theta\rightarrow\infty\:} {\mathrm{lim}}\:\theta^{\mathrm{2}} \left[\mathrm{2sin}\:^{\mathrm{2}} \:\frac{\mathrm{1}}{\theta}\:\right] \\ $$$$\:\:\:\:\:\:=\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\theta^{\mathrm{2}} }\right)\left(\mathrm{2sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:=\mathrm{2}\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:=\mathrm{2}\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right)}{\theta^{\mathrm{2}} }\:=\mathrm{2}×\mathrm{1}=\mathrm{2}// \\ $$
