Question Number 151596 by mathdanisur last updated on 22/Aug/21

Answered by dumitrel last updated on 22/Aug/21
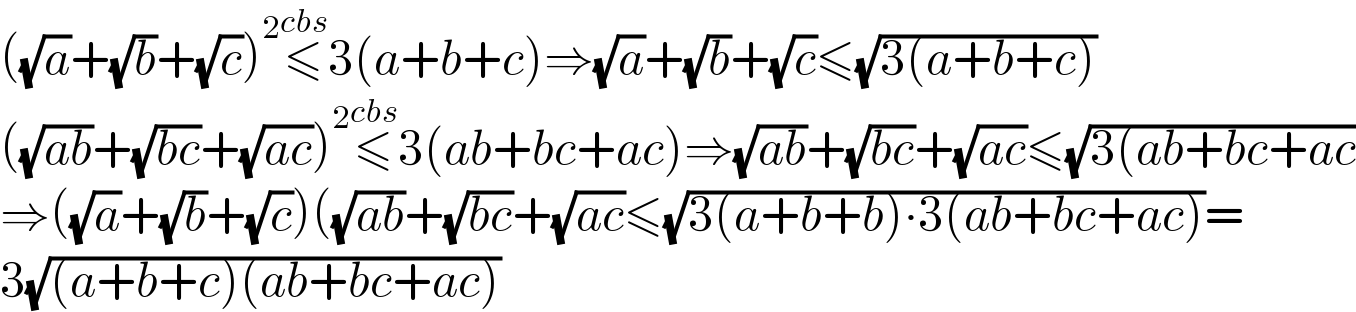
$$\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right)^{\mathrm{2}} \overset{{cbs}} {\leqslant}\mathrm{3}\left({a}+{b}+{c}\right)\Rightarrow\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\leqslant\sqrt{\mathrm{3}\left({a}+{b}+{c}\right)} \\ $$$$\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ac}}\right)^{\mathrm{2}} \overset{{cbs}} {\leqslant}\mathrm{3}\left({ab}+{bc}+{ac}\right)\Rightarrow\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ac}}\leqslant\sqrt{\mathrm{3}\left({ab}+{bc}+{ac}\right.} \\ $$$$\Rightarrow\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right)\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ac}}\leqslant\sqrt{\mathrm{3}\left({a}+{b}+{b}\right)\centerdot\mathrm{3}\left({ab}+{bc}+{ac}\right)}=\right. \\ $$$$\mathrm{3}\sqrt{\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ac}\right)} \\ $$
Commented by mathdanisur last updated on 22/Aug/21
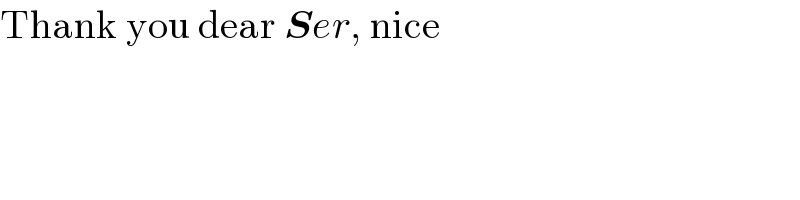
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{{S}}{er},\:\mathrm{nice} \\ $$
