Question Number 151609 by mathdanisur last updated on 22/Aug/21

Answered by ghimisi last updated on 22/Aug/21
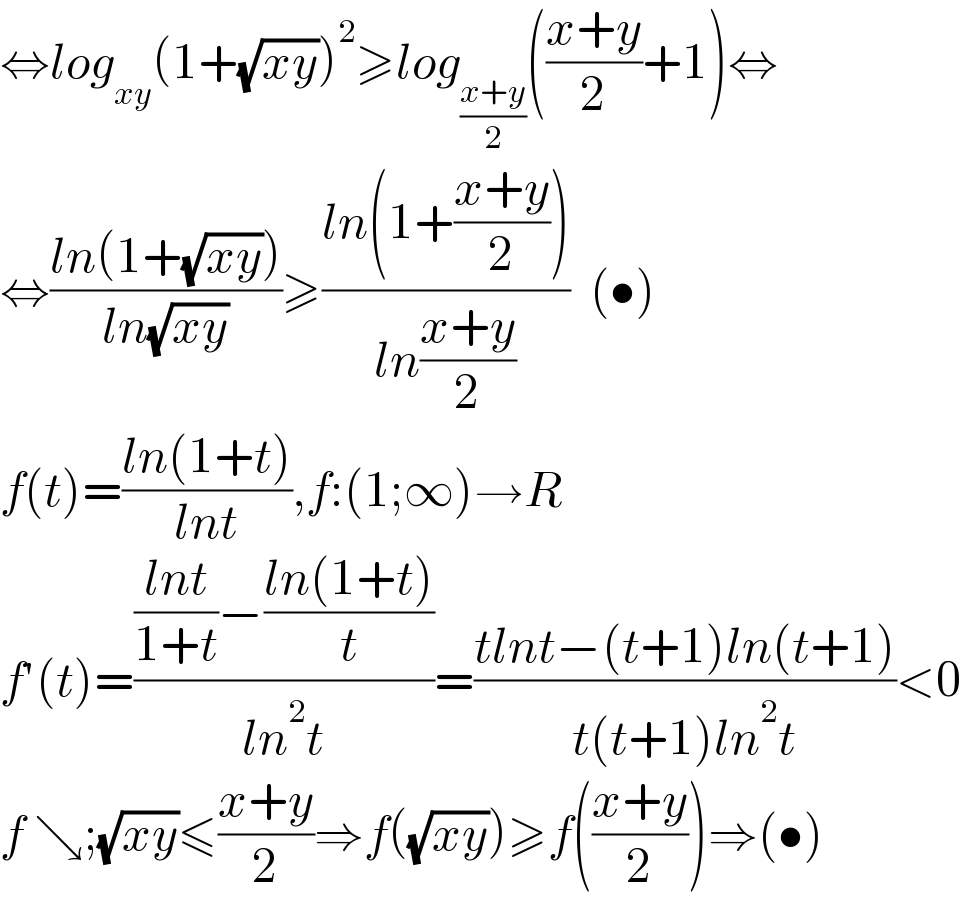
$$\Leftrightarrow{log}_{{xy}} \left(\mathrm{1}+\sqrt{{xy}}\right)^{\mathrm{2}} \geqslant{log}_{\frac{{x}+{y}}{\mathrm{2}}} \left(\frac{{x}+{y}}{\mathrm{2}}+\mathrm{1}\right)\Leftrightarrow \\ $$$$\Leftrightarrow\frac{{ln}\left(\mathrm{1}+\sqrt{{xy}}\right)}{{ln}\sqrt{{xy}}}\geqslant\frac{{ln}\left(\mathrm{1}+\frac{{x}+{y}}{\mathrm{2}}\right)}{{ln}\frac{{x}+{y}}{\mathrm{2}}}\:\:\left(\bullet\right) \\ $$$${f}\left({t}\right)=\frac{{ln}\left(\mathrm{1}+{t}\right)}{{lnt}},{f}:\left(\mathrm{1};\infty\right)\rightarrow{R} \\ $$$${f}'\left({t}\right)=\frac{\frac{{lnt}}{\mathrm{1}+{t}}−\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}}{{ln}^{\mathrm{2}} {t}}=\frac{{tlnt}−\left({t}+\mathrm{1}\right){ln}\left({t}+\mathrm{1}\right)}{{t}\left({t}+\mathrm{1}\right){ln}^{\mathrm{2}} {t}}<\mathrm{0} \\ $$$${f}\:\searrow;\sqrt{{xy}}\leqslant\frac{{x}+{y}}{\mathrm{2}}\Rightarrow{f}\left(\sqrt{{xy}}\right)\geqslant{f}\left(\frac{{x}+{y}}{\mathrm{2}}\right)\Rightarrow\left(\bullet\right) \\ $$
Commented by mathdanisur last updated on 22/Aug/21
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{cool} \\ $$
