Menu Close

Question-151636

Tinku Tara 0 Comments
Pin




Question Number 151636 by Tawa11 last updated on 22/Aug/21
Commented by mr W last updated on 22/Aug/21
do you know the psi−function and ψ(1+z)=−γ+Σ_(n=1) ^∞ ((1/n)−(1/(n+z))) ? if not, then you should learn this at first. Σ_(n=0) ^∞ (1/((n+α)(n+β))) =(1/(β−α))Σ_(n=0) ^∞ [(1/(n+α))−(1/(n+β))] =(1/(β−α)){Σ_(n=0) ^∞ [(1/(n+α))]−Σ_(n=0) ^∞ [(1/(n+β))]} =(1/(β−α)){Σ_(n=1) ^∞ [(1/(n+(α−1)))]−Σ_(n=1) ^∞ [(1/(n+(β−1)))]} =(1/(β−α)){−γ+Σ_(n=1) ^∞ (1/n)−ψ(1+(α−1))−[−γ+Σ_(n=1) ^∞ (1/n)−ψ(1+(β−1))]} =(1/(β−α)){ψ(β)−ψ(α)}
$${do}\:{you}\:{know}\:{the}\:{psi}−{function}\:{and} \\ $$$$\psi\left(\mathrm{1}+{z}\right)=−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+{z}}\right)\:? \\ $$$${if}\:{not},\:{then}\:{you}\:{should}\:{learn}\:{this}\:{at} \\ $$$${first}.\: \\ $$$$ \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\alpha\right)\left({n}+\beta\right)} \\ $$$$=\frac{\mathrm{1}}{\beta−\alpha}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\alpha}−\frac{\mathrm{1}}{{n}+\beta}\right] \\ $$$$=\frac{\mathrm{1}}{\beta−\alpha}\left\{\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\alpha}\right]−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\beta}\right]\right\} \\ $$$$=\frac{\mathrm{1}}{\beta−\alpha}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\left(\alpha−\mathrm{1}\right)}\right]−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{{n}+\left(\beta−\mathrm{1}\right)}\right]\right\} \\ $$$$=\frac{\mathrm{1}}{\beta−\alpha}\left\{−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\psi\left(\mathrm{1}+\left(\alpha−\mathrm{1}\right)\right)−\left[−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}−\psi\left(\mathrm{1}+\left(\beta−\mathrm{1}\right)\right)\right]\right\} \\ $$$$=\frac{\mathrm{1}}{\beta−\alpha}\left\{\psi\left(\beta\right)−\psi\left(\alpha\right)\right\} \\ $$
Commented by Tawa11 last updated on 22/Aug/21
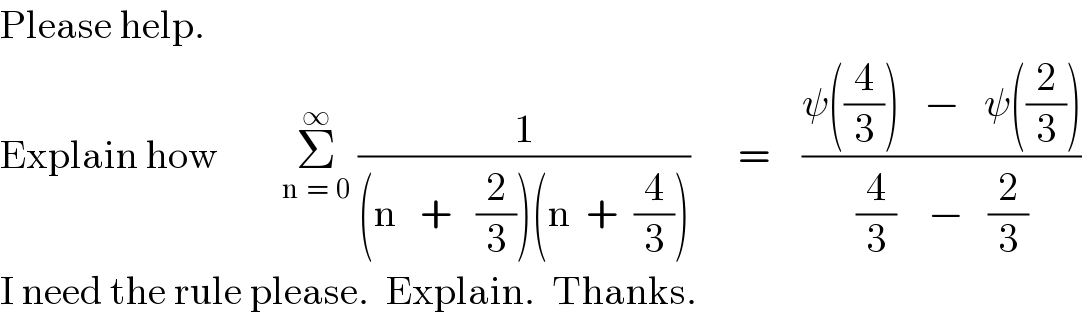
Please help. Explain how Σ_(n = 0) ^∞ (1/((n + (2/3))(n + (4/3)))) = ((ψ((4/3)) − ψ((2/3)))/((4/3) − (2/3))) I need the rule please. Explain. Thanks.
$$\mathrm{Please}\:\mathrm{help}. \\ $$$$\mathrm{Explain}\:\mathrm{how}\:\:\:\:\:\:\:\:\underset{\mathrm{n}\:\:=\:\:\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{n}\:\:\:+\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\right)\left(\mathrm{n}\:\:+\:\:\frac{\mathrm{4}}{\mathrm{3}}\right)}\:\:\:\:\:\:=\:\:\:\:\frac{\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:\:\:−\:\:\:\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\:−\:\:\:\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\mathrm{I}\:\mathrm{need}\:\mathrm{the}\:\mathrm{rule}\:\mathrm{please}.\:\:\mathrm{Explain}.\:\:\mathrm{Thanks}. \\ $$
Commented by Tawa11 last updated on 22/Aug/21
Wow. This is interesting. God bless you sir. Am reading on it. So, I ask the question so that I can read further. Thanks sir. I appreciate.
$$\mathrm{Wow}.\:\mathrm{This}\:\mathrm{is}\:\mathrm{interesting}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{Am}\:\mathrm{reading}\:\mathrm{on}\:\mathrm{it}.\:\mathrm{So},\:\mathrm{I}\:\mathrm{ask}\:\mathrm{the}\:\mathrm{question}\:\mathrm{so}\:\mathrm{that}\:\mathrm{I}\:\mathrm{can}\:\mathrm{read}\:\mathrm{further}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
Commented by Tawa11 last updated on 22/Aug/21
After going through your explanation sir. I understand it perfectly. I am happy. God bless you sir
$$\mathrm{After}\:\mathrm{going}\:\mathrm{through}\:\mathrm{your}\:\mathrm{explanation}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{understand}\:\mathrm{it}\:\mathrm{perfectly}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{happy}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Olaf_Thorendsen last updated on 22/Aug/21
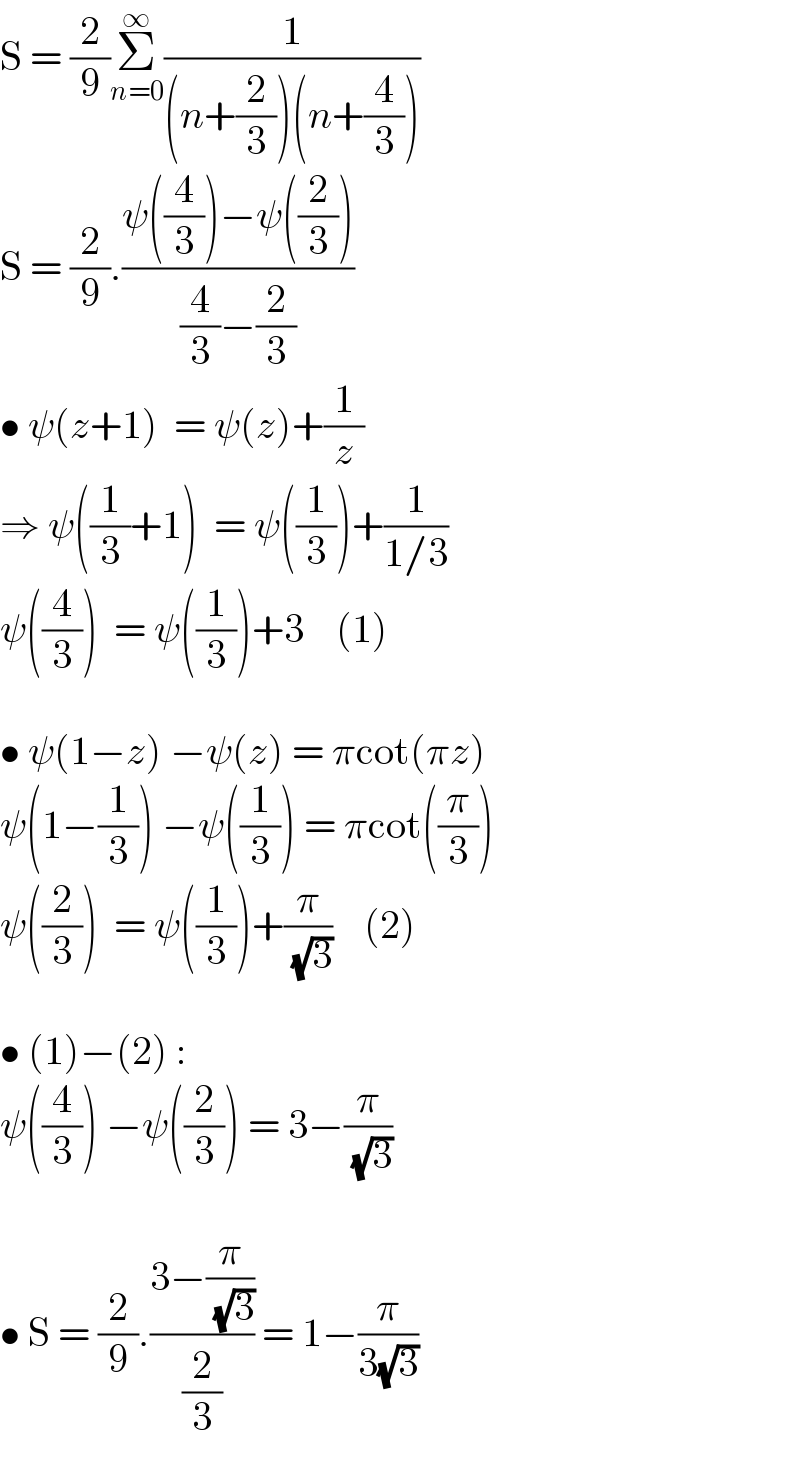
S = (2/9)Σ_(n=0) ^∞ (1/((n+(2/3))(n+(4/3)))) S = (2/9).((ψ((4/3))−ψ((2/3)))/((4/3)−(2/3))) • ψ(z+1) = ψ(z)+(1/z) ⇒ ψ((1/3)+1) = ψ((1/3))+(1/(1/3)) ψ((4/3)) = ψ((1/3))+3 (1) • ψ(1−z) −ψ(z) = πcot(πz) ψ(1−(1/3)) −ψ((1/3)) = πcot((π/3)) ψ((2/3)) = ψ((1/3))+(π/( (√3))) (2) • (1)−(2) : ψ((4/3)) −ψ((2/3)) = 3−(π/( (√3))) • S = (2/9).((3−(π/( (√3))))/(2/3)) = 1−(π/(3(√3)))
$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{4}}{\mathrm{3}}\right)} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}.\frac{\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\bullet\:\psi\left({z}+\mathrm{1}\right)\:\:=\:\psi\left({z}\right)+\frac{\mathrm{1}}{{z}} \\ $$$$\Rightarrow\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{1}/\mathrm{3}} \\ $$$$\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{3}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\bullet\:\psi\left(\mathrm{1}−{z}\right)\:−\psi\left({z}\right)\:=\:\pi\mathrm{cot}\left(\pi{z}\right) \\ $$$$\psi\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)\:−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\pi\mathrm{cot}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}}\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\bullet\:\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:: \\ $$$$\psi\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\:\mathrm{3}−\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$\bullet\:\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{9}}.\frac{\mathrm{3}−\frac{\pi}{\:\sqrt{\mathrm{3}}}}{\frac{\mathrm{2}}{\mathrm{3}}}\:=\:\mathrm{1}−\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by Tawa11 last updated on 22/Aug/21
Wow. Thanks sir. I appreciate. God bless you. I am visiting all your solution in the forum on this. Thank you sir.
$$\mathrm{Wow}.\:\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$$$\mathrm{I}\:\mathrm{am}\:\mathrm{visiting}\:\mathrm{all}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{the}\:\mathrm{forum}\:\mathrm{on}\:\mathrm{this}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *