Question-151660

Question Number 151660 by mathdanisur last updated on 22/Aug/21

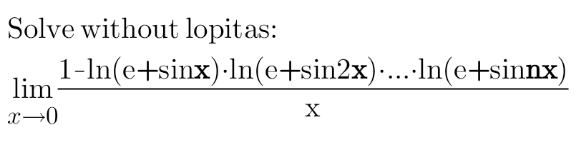
Answered by Olaf_Thorendsen last updated on 22/Aug/21

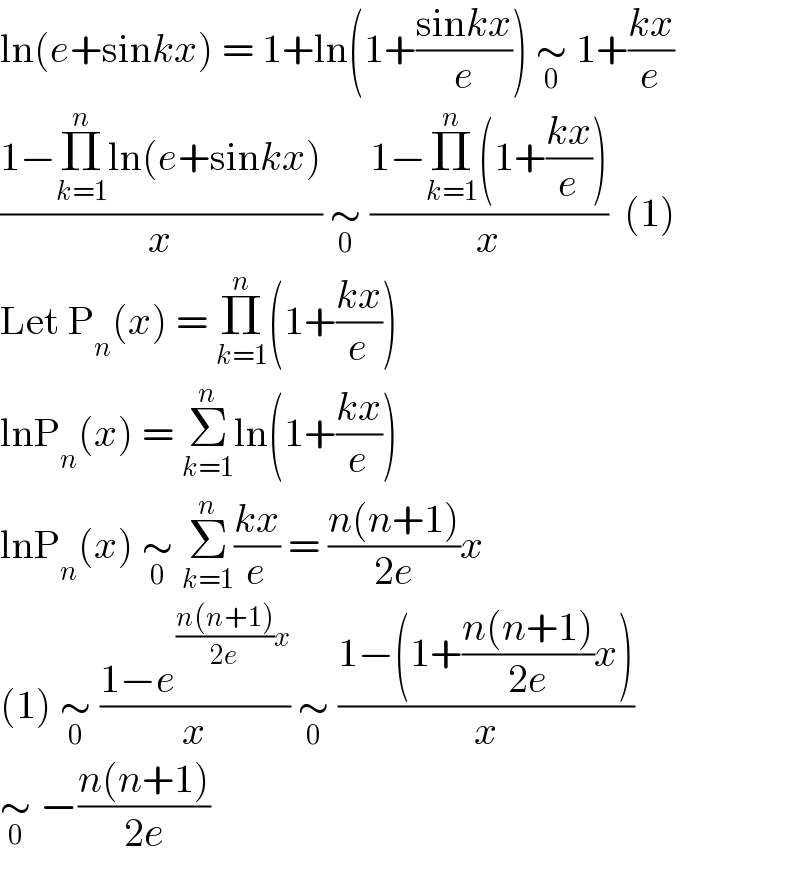
ln(e+sinkx) = 1+ln(1+((sinkx)/e)) ∼_0 1+((kx)/e) ((1−Π_(k=1) ^n ln(e+sinkx))/x) ∼_0 ((1−Π_(k=1) ^n (1+((kx)/e)))/x) (1) Let P_n (x) = Π_(k=1) ^n (1+((kx)/e)) lnP_n (x) = Σ_(k=1) ^n ln(1+((kx)/e)) lnP_n (x) ∼_0 Σ_(k=1) ^n ((kx)/e) = ((n(n+1))/(2e))x (1) ∼_0 ((1−e^(((n(n+1))/(2e))x) )/x) ∼_0 ((1−(1+((n(n+1))/(2e))x))/x) ∼_0 −((n(n+1))/(2e))

$$\mathrm{ln}\left({e}+\mathrm{sin}{kx}\right)\:=\:\mathrm{1}+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{sin}{kx}}{{e}}\right)\:\underset{\mathrm{0}} {\sim}\:\mathrm{1}+\frac{{kx}}{{e}} \\ $$$$\frac{\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{ln}\left({e}+\mathrm{sin}{kx}\right)}{{x}}\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{kx}}{{e}}\right)}{{x}}\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:\mathrm{P}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{kx}}{{e}}\right) \\ $$$$\mathrm{lnP}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{{kx}}{{e}}\right) \\ $$$$\mathrm{lnP}_{{n}} \left({x}\right)\:\underset{\mathrm{0}} {\sim}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{kx}}{{e}}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{e}}{x} \\ $$$$\left(\mathrm{1}\right)\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}−{e}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{e}}{x}} }{{x}}\:\underset{\mathrm{0}} {\sim}\:\frac{\mathrm{1}−\left(\mathrm{1}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{e}}{x}\right)}{{x}} \\ $$$$\underset{\mathrm{0}} {\sim}\:−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{e}} \\ $$

Commented by mathdanisur last updated on 23/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply