Question Number 151766 by mathdanisur last updated on 22/Aug/21

Commented by tabata last updated on 23/Aug/21
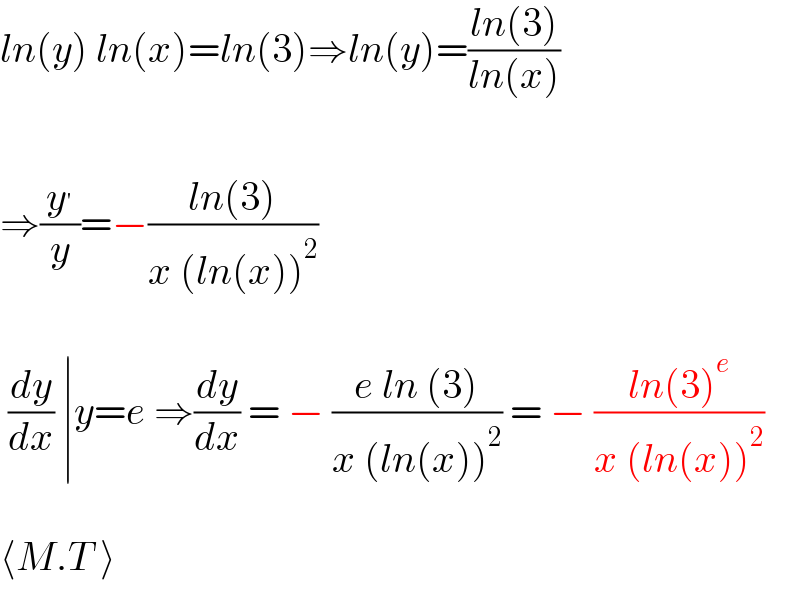
$${ln}\left({y}\right)\:{ln}\left({x}\right)={ln}\left(\mathrm{3}\right)\Rightarrow{ln}\left({y}\right)=\frac{{ln}\left(\mathrm{3}\right)}{{ln}\left({x}\right)} \\ $$$$ \\ $$$$\Rightarrow\frac{{y}^{'} }{{y}}=−\frac{{ln}\left(\mathrm{3}\right)}{{x}\:\left({ln}\left({x}\right)\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\:\frac{{dy}}{{dx}}\:\mid{y}={e}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:−\:\frac{{e}\:{ln}\:\left(\mathrm{3}\right)}{{x}\:\left({ln}\left({x}\right)\right)^{\mathrm{2}} }\:=\:−\:\frac{{ln}\left(\mathrm{3}\right)^{{e}} }{{x}\:\left({ln}\left({x}\right)\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\langle{M}.{T}\:\rangle \\ $$
