Question Number 151791 by mathdanisur last updated on 23/Aug/21

Answered by ghimisi last updated on 23/Aug/21
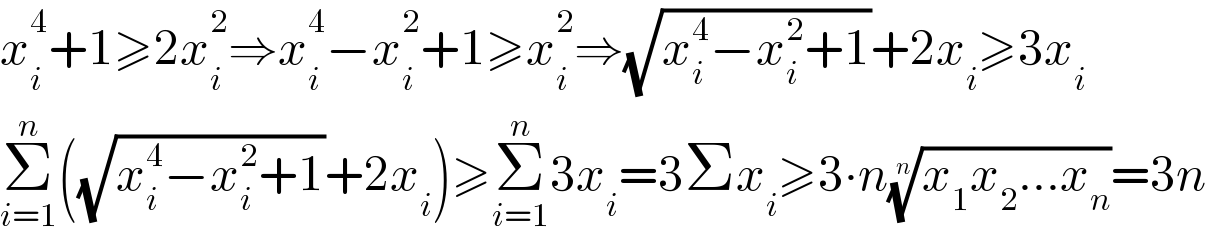
$${x}_{{i}} ^{\mathrm{4}} +\mathrm{1}\geqslant\mathrm{2}{x}_{{i}} ^{\mathrm{2}} \Rightarrow{x}_{{i}} ^{\mathrm{4}} −{x}_{{i}} ^{\mathrm{2}} +\mathrm{1}\geqslant{x}_{{i}} ^{\mathrm{2}} \Rightarrow\sqrt{{x}_{{i}} ^{\mathrm{4}} −{x}_{{i}} ^{\mathrm{2}} +\mathrm{1}}+\mathrm{2}{x}_{{i}} \geqslant\mathrm{3}{x}_{{i}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\sqrt{{x}_{{i}} ^{\mathrm{4}} −{x}_{{i}} ^{\mathrm{2}} +\mathrm{1}}+\mathrm{2}{x}_{{i}} \right)\geqslant\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}{x}_{{i}} =\mathrm{3}\Sigma{x}_{{i}} \geqslant\mathrm{3}\centerdot{n}\sqrt[{{n}}]{{x}_{\mathrm{1}} {x}_{\mathrm{2}} …{x}_{{n}} }=\mathrm{3}{n} \\ $$
Commented by mathdanisur last updated on 23/Aug/21
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{nice} \\ $$
