Question Number 151823 by DELETED last updated on 23/Aug/21
Answered by DELETED last updated on 23/Aug/21

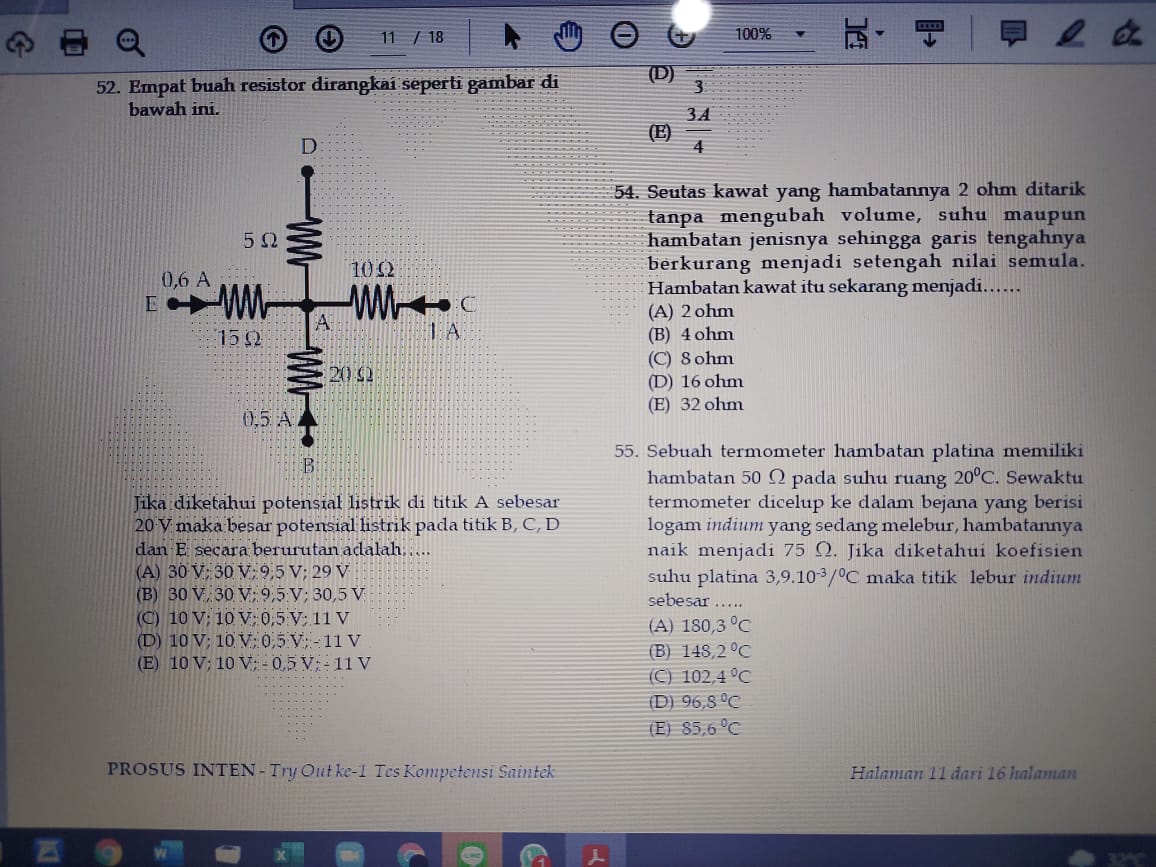
$$\mathrm{54}.\:\:\mathrm{R}_{\mathrm{1}} :\mathrm{R}_{\mathrm{2}} =\rho\frac{\mathrm{l}_{\mathrm{1}} }{\pi\mathrm{R}_{\mathrm{1}} ^{\mathrm{2}} }:\rho\frac{\mathrm{l}_{\mathrm{2}} }{\pi\mathrm{R}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\mathrm{R}_{\mathrm{1}} :\mathrm{R}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{D}_{\mathrm{1}} ^{\mathrm{2}} }\::\:\frac{\mathrm{1}}{\mathrm{D}_{\mathrm{2}} ^{\mathrm{2}} }\:\:\:\mathrm{dan}\:\mathrm{D}_{\mathrm{2}} =\frac{\mathrm{D}_{\mathrm{1}} }{\mathrm{2}} \\ $$$$\:\:\mathrm{2}\::\:\mathrm{R}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{D}_{\mathrm{1}} ^{\mathrm{2}} }\::\:\frac{\mathrm{4}}{\mathrm{D}_{\mathrm{1}} ^{\mathrm{2}} }\: \\ $$$$\:\:\mathrm{2}:\mathrm{R}_{\mathrm{2}} =\mathrm{1}:\mathrm{4}\:\rightarrow\mathrm{R}_{\mathrm{2}} =\mathrm{8}\:\Omega \\ $$
Answered by DELETED last updated on 23/Aug/21

$$\left.\mathrm{55}\right).\:\mathrm{R}_{\mathrm{t}} =\mathrm{R}\left(\mathrm{1}+\alpha.\Delta\mathrm{T}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{75}=\mathrm{50}\left(\mathrm{1}+\mathrm{3},\mathrm{9}×\mathrm{10}^{−\mathrm{3}} .\Delta\mathrm{T}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{75}}{\mathrm{50}}=\mathrm{1}+\mathrm{3},\mathrm{9}×\mathrm{10}^{−\mathrm{3}} .\Delta\mathrm{T} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{1},\mathrm{5}−\mathrm{1}=\mathrm{3},\mathrm{9}×\mathrm{10}^{−\mathrm{3}} .\Delta\mathrm{T} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\Delta\mathrm{T}=\frac{\mathrm{0},\mathrm{5}}{\mathrm{3},\mathrm{9}×\mathrm{10}^{−\mathrm{3}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5000}}{\mathrm{39}}=\mathrm{128},\mathrm{2}\:°\mathrm{C} \\ $$$$\rightarrow\mathrm{Titik}\:\mathrm{lebur}=\mathrm{128},\mathrm{2}+\mathrm{20}=\mathrm{148},\mathrm{2}\:°\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
