Question Number 151849 by mathdanisur last updated on 23/Aug/21
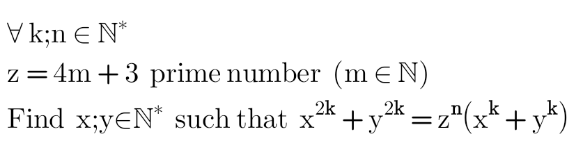
Commented by Rasheed.Sindhi last updated on 23/Aug/21

$${Special}\:{general}\:{case} \\ $$$${x}={y}={z}\left({prime}\:{of}\:\mathrm{4}{m}+\mathrm{3}\:{type}\right) \\ $$$$\frac{{z}^{\mathrm{2}{k}} +{z}^{\mathrm{2}{k}} }{{z}^{{k}} +{z}^{{k}} }=\frac{\mathrm{2}{z}^{\mathrm{2}{k}} }{\mathrm{2}{z}^{{k}} }={z}^{\mathrm{2}{k}−{k}} ={z}^{{k}} ={z}^{{n}} \Rightarrow{k}={n} \\ $$$${x}={y}={z}\left({prime}\:{of}\:\mathrm{4}{m}+\mathrm{3}\:{type}\right)\:\wedge\:{n}={k} \\ $$$${For}\:{example}: \\ $$$${x}={y}={z}=\mathrm{7}=\mathrm{4}\left(\mathrm{1}\right)+\mathrm{3}\:\wedge\:{n}={k} \\ $$$${x}^{\mathrm{2}{k}} +{y}^{\mathrm{2}{k}} ={z}^{{n}} \left({x}^{{k}} +{y}^{{k}} \right) \\ $$$$\Rightarrow\mathrm{7}^{\mathrm{2}{k}} +\mathrm{7}^{\mathrm{2}{k}} =\mathrm{7}^{{k}} \left(\mathrm{7}^{{k}} +\mathrm{7}^{{k}} \right) \\ $$$$\Rightarrow\mathrm{7}^{\mathrm{2}{k}} +\mathrm{7}^{\mathrm{2}{k}} =\mathrm{7}^{\mathrm{2}{k}} +\mathrm{7}^{\mathrm{2}{k}} \\ $$
Commented by mathdanisur last updated on 23/Aug/21

$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
