Question Number 151851 by Tawa11 last updated on 23/Aug/21
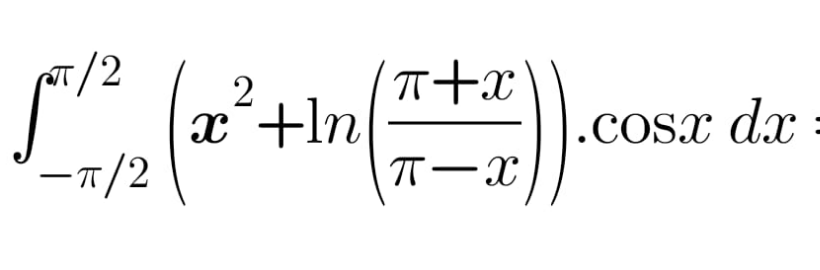
Answered by OlafThorendsen last updated on 23/Aug/21
![I = ∫_(−(π/2)) ^(+(π/2)) (x^2 +ln(((π+x)/(π−x))))cosx dx (1) Let u = −x : I = ∫_(−(π/2)) ^(+(π/2)) (u^2 +ln(((π−u)/(π+u))))cosu du I = ∫_(−(π/2)) ^(+(π/2)) (u^2 −ln(((π+u)/(π−u))))cosu du (2) (((1)+(2))/2) : I = ∫_(−(π/2)) ^(+(π/2)) u^2 cosu du I = [x^2 sinx−2sinx+2xcosx]_(−(π/2)) ^(+(π/2)) I = (π^2 /2)−4](https://www.tinkutara.com/question/Q151873.png)
$$\mathrm{I}\:=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} \left({x}^{\mathrm{2}} +\mathrm{ln}\left(\frac{\pi+{x}}{\pi−{x}}\right)\right)\mathrm{cos}{x}\:{dx}\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Let}\:{u}\:=\:−{x}\:: \\ $$$$\mathrm{I}\:=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} \left({u}^{\mathrm{2}} +\mathrm{ln}\left(\frac{\pi−{u}}{\pi+{u}}\right)\right)\mathrm{cos}{u}\:{du} \\ $$$$\mathrm{I}\:=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} \left({u}^{\mathrm{2}} −\mathrm{ln}\left(\frac{\pi+{u}}{\pi−{u}}\right)\right)\mathrm{cos}{u}\:{du}\:\:\left(\mathrm{2}\right) \\ $$$$\frac{\left(\mathrm{1}\right)+\left(\mathrm{2}\right)}{\mathrm{2}}\::\:\mathrm{I}\:=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} {u}^{\mathrm{2}} \mathrm{cos}{u}\:{du} \\ $$$$\mathrm{I}\:=\:\left[{x}^{\mathrm{2}} \mathrm{sin}{x}−\mathrm{2sin}{x}+\mathrm{2}{x}\mathrm{cos}{x}\right]_{−\frac{\pi}{\mathrm{2}}} ^{+\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{4} \\ $$
Commented by Tawa11 last updated on 23/Aug/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by peter frank last updated on 24/Aug/21

$$\mathrm{good} \\ $$
