Menu Close

Question-151858

Tinku Tara 0 Comments
Pin




Question Number 151858 by mathdanisur last updated on 23/Aug/21
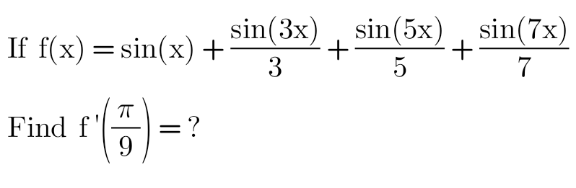
Answered by Olaf_Thorendsen last updated on 23/Aug/21
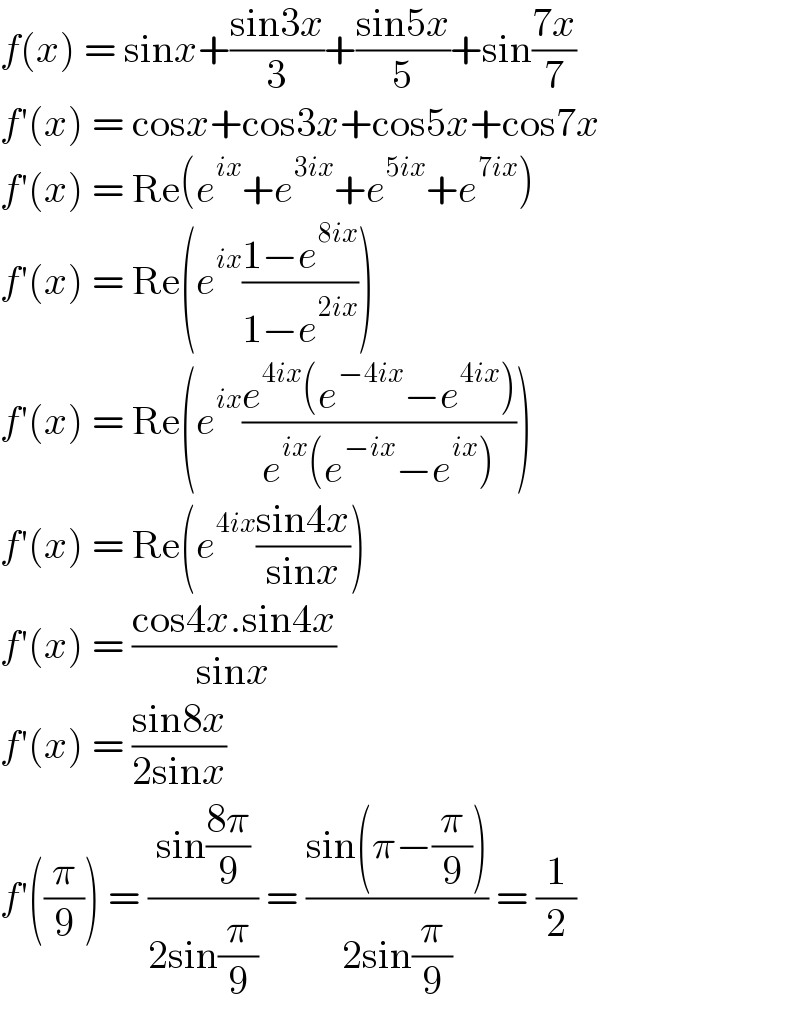
f(x) = sinx+((sin3x)/3)+((sin5x)/5)+sin((7x)/7) f′(x) = cosx+cos3x+cos5x+cos7x f′(x) = Re(e^(ix) +e^(3ix) +e^(5ix) +e^(7ix) ) f′(x) = Re(e^(ix) ((1−e^(8ix) )/(1−e^(2ix) ))) f′(x) = Re(e^(ix) ((e^(4ix) (e^(−4ix) −e^(4ix) ))/(e^(ix) (e^(−ix) −e^(ix) )))) f′(x) = Re(e^(4ix) ((sin4x)/(sinx))) f′(x) = ((cos4x.sin4x)/(sinx)) f′(x) = ((sin8x)/(2sinx)) f′((π/9)) = ((sin((8π)/9))/(2sin(π/9))) = ((sin(π−(π/9)))/(2sin(π/9))) = (1/2)
$${f}\left({x}\right)\:=\:\mathrm{sin}{x}+\frac{\mathrm{sin3}{x}}{\mathrm{3}}+\frac{\mathrm{sin5}{x}}{\mathrm{5}}+\mathrm{sin}\frac{\mathrm{7}{x}}{\mathrm{7}} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{cos}{x}+\mathrm{cos3}{x}+\mathrm{cos5}{x}+\mathrm{cos7}{x} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{Re}\left({e}^{{ix}} +{e}^{\mathrm{3}{ix}} +{e}^{\mathrm{5}{ix}} +{e}^{\mathrm{7}{ix}} \right) \\ $$$${f}'\left({x}\right)\:=\:\mathrm{Re}\left({e}^{{ix}} \frac{\mathrm{1}−{e}^{\mathrm{8}{ix}} }{\mathrm{1}−{e}^{\mathrm{2}{ix}} }\right) \\ $$$${f}'\left({x}\right)\:=\:\mathrm{Re}\left({e}^{{ix}} \frac{{e}^{\mathrm{4}{ix}} \left({e}^{−\mathrm{4}{ix}} −{e}^{\mathrm{4}{ix}} \right)}{{e}^{{ix}} \left({e}^{−{ix}} −{e}^{{ix}} \right)}\right) \\ $$$${f}'\left({x}\right)\:=\:\mathrm{Re}\left({e}^{\mathrm{4}{ix}} \frac{\mathrm{sin4}{x}}{\mathrm{sin}{x}}\right) \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{cos4}{x}.\mathrm{sin4}{x}}{\mathrm{sin}{x}} \\ $$$${f}'\left({x}\right)\:=\:\frac{\mathrm{sin8}{x}}{\mathrm{2sin}{x}} \\ $$$${f}'\left(\frac{\pi}{\mathrm{9}}\right)\:=\:\frac{\mathrm{sin}\frac{\mathrm{8}\pi}{\mathrm{9}}}{\mathrm{2sin}\frac{\pi}{\mathrm{9}}}\:=\:\frac{\mathrm{sin}\left(\pi−\frac{\pi}{\mathrm{9}}\right)}{\mathrm{2sin}\frac{\pi}{\mathrm{9}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 23/Aug/21
Thank You Ser
$$\mathrm{Thank}\:\mathrm{You}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
Commented by Olaf_Thorendsen last updated on 24/Aug/21
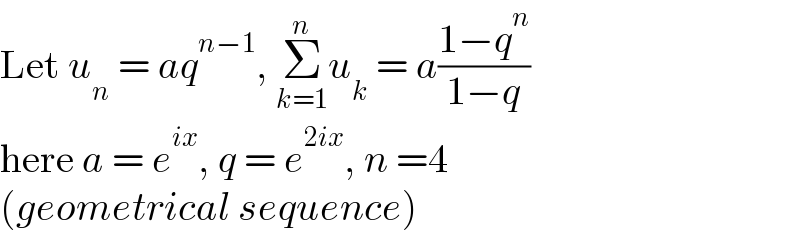
Let u_n = aq^(n−1) , Σ_(k=1) ^n u_k = a((1−q^n )/(1−q)) here a = e^(ix) , q = e^(2ix) , n =4 (geometrical sequence)
$$\mathrm{Let}\:{u}_{{n}} \:=\:{aq}^{{n}−\mathrm{1}} ,\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{u}_{{k}} \:=\:{a}\frac{\mathrm{1}−{q}^{{n}} }{\mathrm{1}−{q}} \\ $$$$\mathrm{here}\:{a}\:=\:{e}^{{ix}} ,\:{q}\:=\:{e}^{\mathrm{2}{ix}} ,\:{n}\:=\mathrm{4} \\ $$$$\left({geometrical}\:{sequence}\right) \\ $$
Commented by mathdanisur last updated on 24/Aug/21
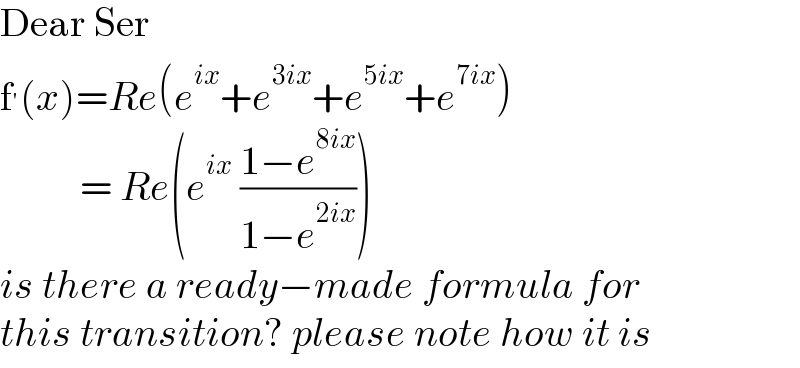
Dear Ser f^′ (x)=Re(e^(ix) +e^(3ix) +e^(5ix) +e^(7ix) ) = Re(e^(ix) ((1−e^(8ix) )/(1−e^(2ix) ))) is there a ready−made formula for this transition? please note how it is
$$\mathrm{Dear}\:\mathrm{Ser} \\ $$$$\mathrm{f}^{'} \left({x}\right)={Re}\left({e}^{{ix}} +{e}^{\mathrm{3}{ix}} +{e}^{\mathrm{5}{ix}} +{e}^{\mathrm{7}{ix}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{Re}\left({e}^{{ix}} \:\frac{\mathrm{1}−{e}^{\mathrm{8}{ix}} }{\mathrm{1}−{e}^{\mathrm{2}{ix}} }\right) \\ $$$${is}\:{there}\:{a}\:{ready}−{made}\:{formula}\:{for} \\ $$$${this}\:{transition}?\:{please}\:{note}\:{how}\:{it}\:{is} \\ $$
Commented by mathdanisur last updated on 24/Aug/21
Thank you Ser
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
Answered by john_santu last updated on 24/Aug/21
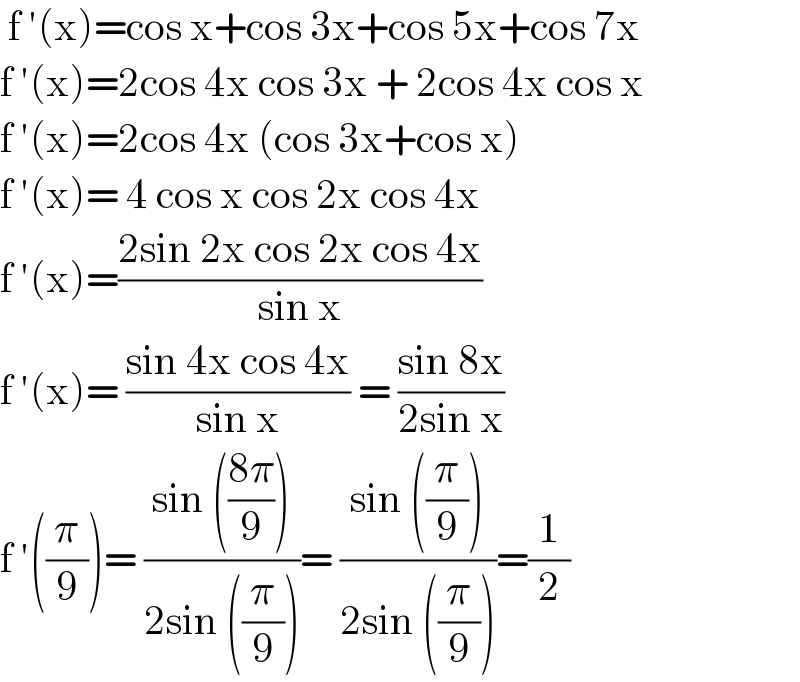
f ′(x)=cos x+cos 3x+cos 5x+cos 7x f ′(x)=2cos 4x cos 3x + 2cos 4x cos x f ′(x)=2cos 4x (cos 3x+cos x) f ′(x)= 4 cos x cos 2x cos 4x f ′(x)=((2sin 2x cos 2x cos 4x)/(sin x)) f ′(x)= ((sin 4x cos 4x)/(sin x)) = ((sin 8x)/(2sin x)) f ′((π/9))= ((sin (((8π)/9)))/(2sin ((π/9))))= ((sin ((π/9)))/(2sin ((π/9))))=(1/2)
$$\:\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{cos}\:\mathrm{x}+\mathrm{cos}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{5x}+\mathrm{cos}\:\mathrm{7x} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2cos}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{3x}\:+\:\mathrm{2cos}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2cos}\:\mathrm{4x}\:\left(\mathrm{cos}\:\mathrm{3x}+\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\:\mathrm{4}\:\mathrm{cos}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{4x}\: \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\mathrm{2sin}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{2x}\:\mathrm{cos}\:\mathrm{4x}}{\mathrm{sin}\:\mathrm{x}}\: \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\:\frac{\mathrm{sin}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{4x}}{\mathrm{sin}\:\mathrm{x}}\:=\:\frac{\mathrm{sin}\:\mathrm{8x}}{\mathrm{2sin}\:\mathrm{x}} \\ $$$$\mathrm{f}\:'\left(\frac{\pi}{\mathrm{9}}\right)=\:\frac{\mathrm{sin}\:\left(\frac{\mathrm{8}\pi}{\mathrm{9}}\right)}{\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{9}}\right)}=\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{9}}\right)}{\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{9}}\right)}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 24/Aug/21
Thank you Ser
$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *