Question Number 151859 by puissant last updated on 23/Aug/21
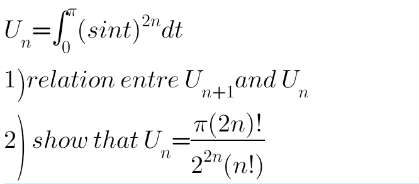
Commented by OlafThorendsen last updated on 23/Aug/21
![1) U_n = ∫_0 ^π sin^(2n) t dt U_0 = ∫_0 ^π dt = π and ∀n≥0, U_(n+1) = ∫_0 ^π sin^(2n+2) t dt U_(n+1) = ∫_0 ^π sint.sin^(2n+1) t dt U_(n+1) = [−cost.sin^(2n+1) t]_0 ^π −∫_0 ^π (−cost)(2n+1)costsin^(2n) t dt U_(n+1) = (2n+1)∫_0 ^π cos^2 tsin^(2n) t dt U_(n+1) = (2n+1)∫_0 ^π (1−sin^2 t)sin^(2n) t dt U_(n+1) = (2n+1)(U_n −U_(n+1) ) U_(n+1) = ((2n+1)/(2n+2))U_n (1) 2) (1) : U_n = ((2n−1)/(2n))U_(n−1) = ... = ((Π_(k=1) ^n (2k−1))/(2^n n!))U_0 U_n = ((Π_(k=1) ^n (2k−1))/(2^n n!))×((Π_(k=1) ^n (2k))/(2^n n!))π U_n = ((π(2n)!)/(2^(2n) n!^2 )) Attention ! Au denominateur c′est n!^2 et non n!](https://www.tinkutara.com/question/Q151872.png)
$$\left.\mathrm{1}\right) \\ $$$${U}_{{n}} \:=\:\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{2}{n}} {t}\:{dt} \\ $$$${U}_{\mathrm{0}} \:=\:\int_{\mathrm{0}} ^{\pi} {dt}\:=\:\pi\:\mathrm{and}\: \\ $$$$\forall{n}\geqslant\mathrm{0},\:{U}_{{n}+\mathrm{1}} \:=\:\int_{\mathrm{0}} ^{\pi} \mathrm{sin}^{\mathrm{2}{n}+\mathrm{2}} {t}\:{dt} \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\int_{\mathrm{0}} ^{\pi} \mathrm{sin}{t}.\mathrm{sin}^{\mathrm{2}{n}+\mathrm{1}} {t}\:{dt} \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\left[−\mathrm{cos}{t}.\mathrm{sin}^{\mathrm{2}{n}+\mathrm{1}} {t}\right]_{\mathrm{0}} ^{\pi} \\ $$$$−\int_{\mathrm{0}} ^{\pi} \left(−\mathrm{cos}{t}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{cos}{t}\mathrm{sin}^{\mathrm{2}{n}} {t}\:{dt} \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\left(\mathrm{2}{n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\pi} \mathrm{cos}^{\mathrm{2}} {t}\mathrm{sin}^{\mathrm{2}{n}} {t}\:{dt} \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\left(\mathrm{2}{n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {t}\right)\mathrm{sin}^{\mathrm{2}{n}} {t}\:{dt} \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\left(\mathrm{2}{n}+\mathrm{1}\right)\left({U}_{{n}} −{U}_{{n}+\mathrm{1}} \right) \\ $$$${U}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}{U}_{{n}} \:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\::\:{U}_{{n}} \:=\:\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}{U}_{{n}−\mathrm{1}} \:=\:…\:=\:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}−\mathrm{1}\right)}{\mathrm{2}^{{n}} {n}!}{U}_{\mathrm{0}} \\ $$$${U}_{{n}} \:=\:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}−\mathrm{1}\right)}{\mathrm{2}^{{n}} {n}!}×\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{2}{k}\right)}{\mathrm{2}^{{n}} {n}!}\pi \\ $$$${U}_{{n}} \:=\:\frac{\pi\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} {n}!^{\mathrm{2}} } \\ $$$$\mathrm{Attention}\:! \\ $$$$\mathrm{Au}\:\mathrm{denominateur}\:\mathrm{c}'\mathrm{est}\:{n}!^{\mathrm{2}} \\ $$$$\mathrm{et}\:\mathrm{non}\:{n}! \\ $$
Commented by puissant last updated on 23/Aug/21

$${oui}\:{Mr}\:{vous}\:{connaissez}.. \\ $$$${c}'{est}\:{moi}\:{qui}\:{commet}\:{l}'{erreur}.. \\ $$$${bravooo}\:{Mr}\:{c}'{est}\:{jolie}\:{comme}\:{solution}. \\ $$
