Question Number 15212 by ajfour last updated on 08/Jun/17
Commented by ajfour last updated on 08/Jun/17

$${Solution}\:{to}\:{Q}.\mathrm{15175} \\ $$
Answered by ajfour last updated on 08/Jun/17
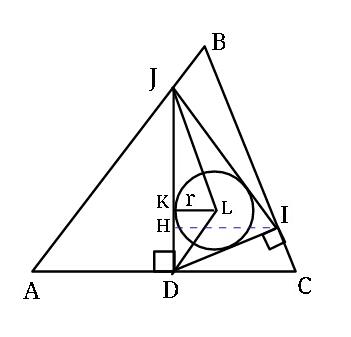
![CD=(b/2), AD=(b/2) ∠HDI+∠CDI=(π/2) ∠HDI+(π/2)−∠C=(π/2) ⇒∠HDI=∠C ∠HDL=(C/2) HD =(b/2)sin Ccos C HI=(b/2)sin^2 C JD=(b/2)tan A , JH=JD−HD JH=(b/2)(tan A−sin Ccos C) ∠IJH=𝛂 , tan α=((HI)/(JH)) tan α=((sin^2 C)/(tan A−sin Ccos C)) ....(i) ∠KJL=(α/2) JK+KD=JD (r/(tan (𝛂/2)))+(r/(tan (C/2)))=(b/2)tan A so, r=(b/2)tan A[((tan (𝛂/2)tan (C/2))/(tan (𝛂/2)+tan (C/2)))] ......... .......... ......... cos A=((b^2 +c^2 −a^2 )/(2bc))=((225+196−169)/(2×15×14)) cos A=(3/5) ⇒ tan A=(4/3) cos C=((a^2 +b^2 −c^2 )/(2ab))=((169+225−196)/(2×13×15)) =((33)/(65)). ⇒ sin C=((56)/(65)) and tan C=((56)/(33)) tan α=((sin^2 C)/(tan A−sin Ccos C)) =(((56/65)^2 )/((4/3)−(56/65)(33/65))) tan α= 0.8285 ⇒ α=0.692rad C=tan^(−1) (56/33)=1.0383 r=(((b/2)tan A)/([(1/(tan (α/2)))+(1/(tan (C/2))])) = (((((15)/2)×(4/3)))/([(1/(tan (0.346)))+(1/(tan (0.519)))])) = ((10)/((2.774+1.75)))= 2.21 units •](https://www.tinkutara.com/question/Q15218.png)
$${CD}=\frac{{b}}{\mathrm{2}},\:{AD}=\frac{{b}}{\mathrm{2}} \\ $$$$\angle{HDI}+\angle{CDI}=\frac{\pi}{\mathrm{2}} \\ $$$$\:\angle{HDI}+\frac{\pi}{\mathrm{2}}−\angle{C}=\frac{\pi}{\mathrm{2}}\:\Rightarrow\angle{HDI}=\angle{C} \\ $$$$\angle{HDL}=\frac{{C}}{\mathrm{2}} \\ $$$${HD}\:=\frac{{b}}{\mathrm{2}}\mathrm{sin}\:{C}\mathrm{cos}\:{C} \\ $$$${HI}=\frac{{b}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} {C} \\ $$$${JD}=\frac{{b}}{\mathrm{2}}\mathrm{tan}\:{A}\:,\:\:{JH}={JD}−{HD} \\ $$$${JH}=\frac{{b}}{\mathrm{2}}\left(\mathrm{tan}\:{A}−\mathrm{sin}\:{C}\mathrm{cos}\:{C}\right) \\ $$$$\angle{IJH}=\boldsymbol{\alpha}\:\:,\:\mathrm{tan}\:\alpha=\frac{{HI}}{{JH}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:^{\mathrm{2}} {C}}{\mathrm{tan}\:{A}−\mathrm{sin}\:{C}\mathrm{cos}\:{C}}\:\:\:….\left({i}\right) \\ $$$$\angle{KJL}=\frac{\alpha}{\mathrm{2}} \\ $$$${JK}+{KD}={JD} \\ $$$$\frac{\boldsymbol{{r}}}{\mathrm{tan}\:\left(\boldsymbol{\alpha}/\mathrm{2}\right)}+\frac{\boldsymbol{{r}}}{\mathrm{tan}\:\left(\boldsymbol{{C}}/\mathrm{2}\right)}=\frac{\boldsymbol{{b}}}{\mathrm{2}}\mathrm{tan}\:\boldsymbol{{A}} \\ $$$${so}, \\ $$$$\boldsymbol{{r}}=\frac{\boldsymbol{{b}}}{\mathrm{2}}\mathrm{tan}\:\boldsymbol{{A}}\left[\frac{\mathrm{tan}\:\left(\boldsymbol{\alpha}/\mathrm{2}\right)\mathrm{tan}\:\left(\boldsymbol{{C}}/\mathrm{2}\right)}{\mathrm{tan}\:\left(\boldsymbol{\alpha}/\mathrm{2}\right)+\mathrm{tan}\:\left(\boldsymbol{{C}}/\mathrm{2}\right)}\right] \\ $$$$\:\:\:\:\:\:………\:\:\:\:\:\:\:……….\:\:\:\:\:\:……… \\ $$$$\mathrm{cos}\:{A}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}=\frac{\mathrm{225}+\mathrm{196}−\mathrm{169}}{\mathrm{2}×\mathrm{15}×\mathrm{14}} \\ $$$$\:\mathrm{cos}\:{A}=\frac{\mathrm{3}}{\mathrm{5}}\:\:\Rightarrow\:\mathrm{tan}\:{A}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:{C}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}=\frac{\mathrm{169}+\mathrm{225}−\mathrm{196}}{\mathrm{2}×\mathrm{13}×\mathrm{15}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{33}}{\mathrm{65}}. \\ $$$$\Rightarrow\:\mathrm{sin}\:{C}=\frac{\mathrm{56}}{\mathrm{65}}\:\:{and}\:\mathrm{tan}\:{C}=\frac{\mathrm{56}}{\mathrm{33}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{sin}\:^{\mathrm{2}} {C}}{\mathrm{tan}\:{A}−\mathrm{sin}\:{C}\mathrm{cos}\:{C}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{56}/\mathrm{65}\right)^{\mathrm{2}} }{\left(\mathrm{4}/\mathrm{3}\right)−\left(\mathrm{56}/\mathrm{65}\right)\left(\mathrm{33}/\mathrm{65}\right)} \\ $$$$\mathrm{tan}\:\alpha=\:\mathrm{0}.\mathrm{8285}\:\Rightarrow\:\alpha=\mathrm{0}.\mathrm{692}{rad} \\ $$$${C}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{56}/\mathrm{33}\right)=\mathrm{1}.\mathrm{0383} \\ $$$$\boldsymbol{{r}}=\frac{\left(\boldsymbol{{b}}/\mathrm{2}\right)\mathrm{tan}\:\boldsymbol{{A}}}{\left[\frac{\mathrm{1}}{\mathrm{tan}\:\left(\alpha/\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{tan}\:\left({C}/\mathrm{2}\right.}\right]} \\ $$$$\:\:=\:\:\frac{\left(\frac{\mathrm{15}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}\right)}{\left[\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{0}.\mathrm{346}\right)}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{0}.\mathrm{519}\right)}\right]} \\ $$$$\:\:=\:\frac{\mathrm{10}}{\left(\mathrm{2}.\mathrm{774}+\mathrm{1}.\mathrm{75}\right)}=\:\mathrm{2}.\mathrm{21}\:{units}\:\bullet \\ $$
Commented by mrW1 last updated on 08/Jun/17

$$\mathrm{Tip} \\ $$$$\mathrm{when}\:\mathrm{we}\:\mathrm{know}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}, \\ $$$$\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{its}\:\mathrm{inscribed}\:\mathrm{circle}\:\mathrm{r}_{\mathrm{i}} \\ $$$$\mathrm{can}\:\mathrm{also}\:\mathrm{be}\:\mathrm{calculated}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{A}=\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)} \\ $$$$\mathrm{but} \\ $$$$\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ar}_{\mathrm{i}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{br}_{\mathrm{i}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cr}_{\mathrm{i}} =\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{2}}×\mathrm{r}_{\mathrm{i}} =\mathrm{sr}_{\mathrm{i}} \\ $$$$\Rightarrow\mathrm{r}_{\mathrm{i}} =\frac{\sqrt{\mathrm{s}\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}}{\mathrm{s}}=\sqrt{\frac{\left(\mathrm{s}−\mathrm{a}\right)\left(\mathrm{s}−\mathrm{b}\right)\left(\mathrm{s}−\mathrm{c}\right)}{\mathrm{s}}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 08/Jun/17

$${hello}\:{my}\:{friend}:\:{mr}\:{Ajfour}. \\ $$$${your}\:{solution}\:{is}\:{smart}\:{and}\:{simple}. \\ $$$${i}\:{love}\:{it}\:{so}\:{much}.{thanks}\:{a}\:{lot}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 09/Jun/17
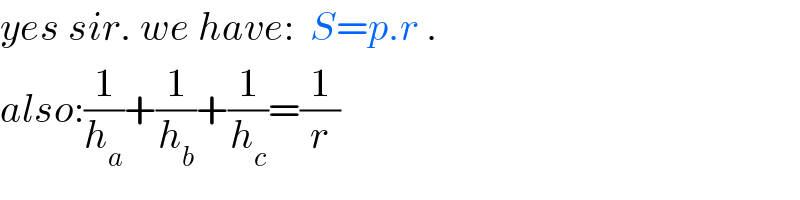
$${yes}\:{sir}.\:{we}\:{have}:\:\:{S}={p}.{r}\:. \\ $$$${also}:\frac{\mathrm{1}}{{h}_{{a}} }+\frac{\mathrm{1}}{{h}_{{b}} }+\frac{\mathrm{1}}{{h}_{{c}} }=\frac{\mathrm{1}}{{r}} \\ $$
