Menu Close

Question-152151

Tinku Tara 0 Comments
Pin




Question Number 152151 by john_santu last updated on 26/Aug/21
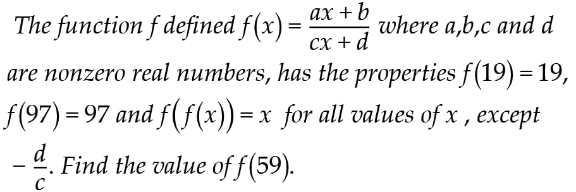
Answered by Rasheed.Sindhi last updated on 26/Aug/21
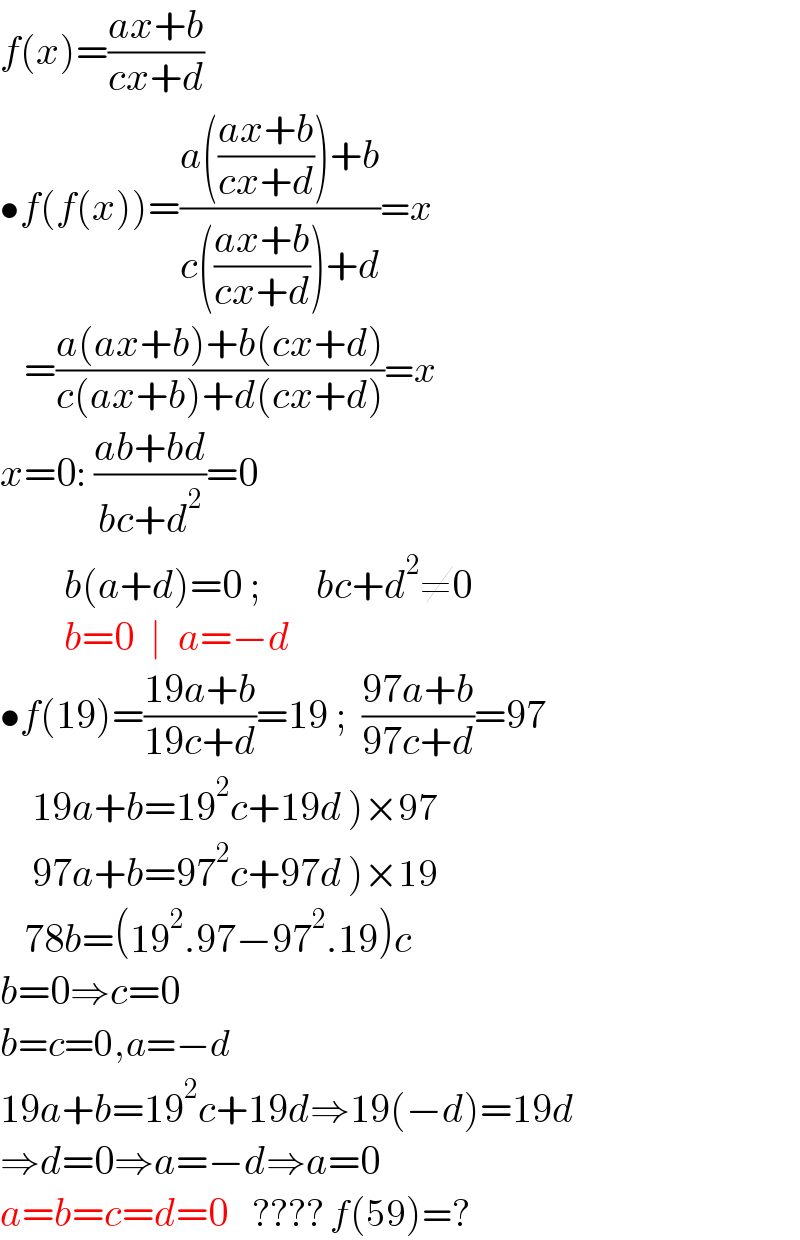
f(x)=((ax+b)/(cx+d)) •f(f(x))=((a(((ax+b)/(cx+d)))+b)/(c(((ax+b)/(cx+d)))+d))=x =((a(ax+b)+b(cx+d))/(c(ax+b)+d(cx+d)))=x x=0: ((ab+bd)/(bc+d^2 ))=0 b(a+d)=0 ; bc+d^2 ≠0 b=0 ∣ a=−d •f(19)=((19a+b)/(19c+d))=19 ; ((97a+b)/(97c+d))=97 19a+b=19^2 c+19d )×97 97a+b=97^2 c+97d )×19 78b=(19^2 .97−97^2 .19)c b=0⇒c=0 b=c=0,a=−d 19a+b=19^2 c+19d⇒19(−d)=19d ⇒d=0⇒a=−d⇒a=0 a=b=c=d=0 ???? f(59)=?
$${f}\left({x}\right)=\frac{{ax}+{b}}{{cx}+{d}} \\ $$$$\bullet{f}\left({f}\left({x}\right)\right)=\frac{{a}\left(\frac{{ax}+{b}}{{cx}+{d}}\right)+{b}}{{c}\left(\frac{{ax}+{b}}{{cx}+{d}}\right)+{d}}={x} \\ $$$$\:\:\:=\frac{{a}\left({ax}+{b}\right)+{b}\left({cx}+{d}\right)}{{c}\left({ax}+{b}\right)+{d}\left({cx}+{d}\right)}={x} \\ $$$${x}=\mathrm{0}:\:\frac{{ab}+{bd}}{{bc}+{d}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{b}\left({a}+{d}\right)=\mathrm{0}\:;\:\:\:\:\:\:\:{bc}+{d}^{\mathrm{2}} \neq\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:{b}=\mathrm{0}\:\:\mid\:\:{a}=−{d} \\ $$$$\bullet{f}\left(\mathrm{19}\right)=\frac{\mathrm{19}{a}+{b}}{\mathrm{19}{c}+{d}}=\mathrm{19}\:;\:\:\frac{\mathrm{97}{a}+{b}}{\mathrm{97}{c}+{d}}=\mathrm{97} \\ $$$$\left.\:\:\:\:\mathrm{19}{a}+{b}=\mathrm{19}^{\mathrm{2}} {c}+\mathrm{19}{d}\:\right)×\mathrm{97} \\ $$$$\left.\:\:\:\:\mathrm{97}{a}+{b}=\mathrm{97}^{\mathrm{2}} {c}+\mathrm{97}{d}\:\right)×\mathrm{19} \\ $$$$\:\:\:\mathrm{78}{b}=\left(\mathrm{19}^{\mathrm{2}} .\mathrm{97}−\mathrm{97}^{\mathrm{2}} .\mathrm{19}\right){c} \\ $$$${b}=\mathrm{0}\Rightarrow{c}=\mathrm{0} \\ $$$${b}={c}=\mathrm{0},{a}=−{d} \\ $$$$\mathrm{19}{a}+{b}=\mathrm{19}^{\mathrm{2}} {c}+\mathrm{19}{d}\Rightarrow\mathrm{19}\left(−{d}\right)=\mathrm{19}{d} \\ $$$$\Rightarrow{d}=\mathrm{0}\Rightarrow{a}=−{d}\Rightarrow{a}=\mathrm{0} \\ $$$${a}={b}={c}={d}=\mathrm{0}\:\:\:\:????\:{f}\left(\mathrm{59}\right)=? \\ $$
Commented by john_santu last updated on 26/Aug/21
no sir.
$$\mathrm{no}\:\mathrm{sir}. \\ $$
Commented by prakash jain last updated on 27/Aug/21
If we put b=d=0 ((19a)/d)=19⇒ a=d f(x)=x b=0 or a=−d so when b=0 a need not be −d
$$\mathrm{If}\:\mathrm{we}\:\mathrm{put}\:\mathrm{b}=\mathrm{d}=\mathrm{0} \\ $$$$\frac{\mathrm{19a}}{\mathrm{d}}=\mathrm{19}\Rightarrow\:\mathrm{a}=\mathrm{d} \\ $$$${f}\left({x}\right)={x} \\ $$$${b}=\mathrm{0}\:\mathrm{or}\:\mathrm{a}=−\mathrm{d} \\ $$$$\mathrm{so}\:\mathrm{when}\:\mathrm{b}=\mathrm{0}\:\mathrm{a}\:\mathrm{need}\:\mathrm{not}\:\mathrm{be}\:−\mathrm{d} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Aug/21
THANKS SIR!
$$\mathrm{THANKS}\:\mathrm{SIR}! \\ $$
Answered by prakash jain last updated on 26/Aug/21
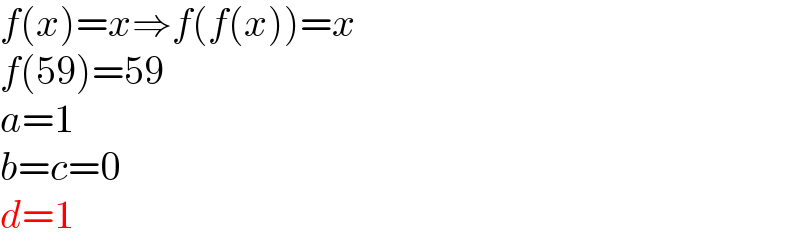
f(x)=x⇒f(f(x))=x f(59)=59 a=1 b=c=0 d=1
$${f}\left({x}\right)={x}\Rightarrow{f}\left({f}\left({x}\right)\right)={x} \\ $$$${f}\left(\mathrm{59}\right)=\mathrm{59} \\ $$$${a}=\mathrm{1} \\ $$$${b}={c}=\mathrm{0} \\ $$$${d}=\mathrm{1} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Aug/21
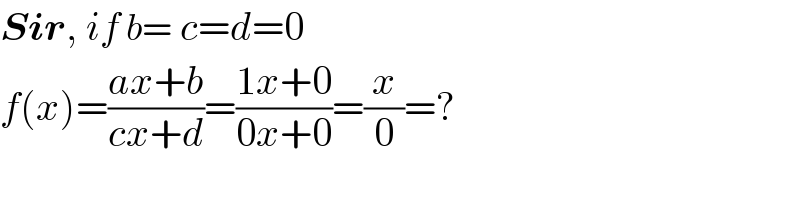
Sir, if b= c=d=0 f(x)=((ax+b)/(cx+d))=((1x+0)/(0x+0))=(x/0)=?
$$\boldsymbol{{Sir}},\:{if}\:{b}=\:{c}={d}=\mathrm{0} \\ $$$${f}\left({x}\right)=\frac{{ax}+{b}}{{cx}+{d}}=\frac{\mathrm{1}{x}+\mathrm{0}}{\mathrm{0}{x}+\mathrm{0}}=\frac{{x}}{\mathrm{0}}=? \\ $$
Commented by prakash jain last updated on 26/Aug/21
Thanks. Correctrd b=c=0 d=1 so that f(x)=x
$$\mathrm{Thanks}. \\ $$$$\mathrm{Correctrd} \\ $$$${b}={c}=\mathrm{0} \\ $$$${d}=\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{that}\:{f}\left({x}\right)={x} \\ $$
Commented by john_santu last updated on 27/Aug/21
wrong sir
$$\mathrm{wrong}\:\mathrm{sir} \\ $$
Commented by prakash jain last updated on 06/Sep/21
You are right. I did not read question properly. Question specifically said a,b,c,d are not zero.
$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{read}\:\mathrm{question} \\ $$$$\mathrm{properly}.\:\mathrm{Question}\:\mathrm{specifically}\:\mathrm{said} \\ $$$$\mathrm{a},{b},{c},{d}\:{are}\:{not}\:{zero}. \\ $$
Answered by john_santu last updated on 27/Aug/21
For all x ,f(f(x))=x ,i.e ((a(((ax+b)/(cx+d)))+b)/(c(((ax+b)/(cx+d)))+d)) = x, i.e (((a^2 +bc)x+b(a+d))/(c(a+d)x+bc+d^2 )) = x , i.e c(a+d)x^2 +(d^2 −a^2 )x−b(a+d)=0, which implies c(a+d)=0 , since c ≠0 we must have a=−d . The conditions f(19)=19 and f(97)=97 lead to the equations { ((19^2 c=2.19a+b)),((97^2 c=2.97a+b)) :} Hence (97^2 −19^2 )c = 2(97−19)a it follows that a=18c ,which in turn leads to b=−1843c therefore f(x)=((58x−1843)/(x−58)) so f(59)=((58×59−1843)/(59−58)) =1579
$$\mathrm{For}\:\mathrm{all}\:\mathrm{x}\:,\mathrm{f}\left(\mathrm{f}\left(\mathrm{x}\right)\right)=\mathrm{x}\:,\mathrm{i}.\mathrm{e}\: \\ $$$$\:\frac{\mathrm{a}\left(\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{cx}+\mathrm{d}}\right)+\mathrm{b}}{\mathrm{c}\left(\frac{\mathrm{ax}+\mathrm{b}}{\mathrm{cx}+\mathrm{d}}\right)+\mathrm{d}}\:=\:\mathrm{x},\:\mathrm{i}.\mathrm{e} \\ $$$$\:\frac{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{bc}\right)\mathrm{x}+\mathrm{b}\left(\mathrm{a}+\mathrm{d}\right)}{\mathrm{c}\left(\mathrm{a}+\mathrm{d}\right)\mathrm{x}+\mathrm{bc}+\mathrm{d}^{\mathrm{2}} }\:=\:\mathrm{x}\:,\:\mathrm{i}.\mathrm{e} \\ $$$$\:\mathrm{c}\left(\mathrm{a}+\mathrm{d}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{d}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)\mathrm{x}−\mathrm{b}\left(\mathrm{a}+\mathrm{d}\right)=\mathrm{0}, \\ $$$$\mathrm{which}\:\mathrm{implies}\:\mathrm{c}\left(\mathrm{a}+\mathrm{d}\right)=\mathrm{0}\:,\:\mathrm{since}\:\mathrm{c}\:\neq\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{have}\:\mathrm{a}=−\mathrm{d}\:.\: \\ $$$$\mathrm{The}\:\mathrm{conditions}\:\mathrm{f}\left(\mathrm{19}\right)=\mathrm{19}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{97}\right)=\mathrm{97} \\ $$$$\mathrm{lead}\:\mathrm{to}\:\mathrm{the}\:\mathrm{equations}\: \\ $$$$\:\begin{cases}{\mathrm{19}^{\mathrm{2}} \:\mathrm{c}=\mathrm{2}.\mathrm{19a}+\mathrm{b}}\\{\mathrm{97}^{\mathrm{2}} \:\mathrm{c}=\mathrm{2}.\mathrm{97a}+\mathrm{b}}\end{cases} \\ $$$$\:\mathrm{Hence}\:\left(\mathrm{97}^{\mathrm{2}} −\mathrm{19}^{\mathrm{2}} \right)\mathrm{c}\:=\:\mathrm{2}\left(\mathrm{97}−\mathrm{19}\right)\mathrm{a} \\ $$$$\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{a}=\mathrm{18c}\:,\mathrm{which}\:\mathrm{in} \\ $$$$\:\mathrm{turn}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{b}=−\mathrm{1843c} \\ $$$$\mathrm{therefore}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{58x}−\mathrm{1843}}{\mathrm{x}−\mathrm{58}} \\ $$$$\mathrm{so}\:\mathrm{f}\left(\mathrm{59}\right)=\frac{\mathrm{58}×\mathrm{59}−\mathrm{1843}}{\mathrm{59}−\mathrm{58}}\:=\mathrm{1579} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *