Question Number 15217 by Mr Chheang Chantria last updated on 08/Jun/17

Answered by ajfour last updated on 08/Jun/17
![v=ab^2 +a^2 b+ac+bc v =ab(a+b)+c(a+b) =(a+b)(ab+c)≤(a+b)[(((a+b)^2 )/4)+c] 4v ≤(1−c)[(1−c)^2 +4c] 4v≤(1−c)(1+c)^2 [=f(x)] ≤max[f(x)] for 0≤x≤1 ∀ f(x)=(1−x)(1+x)^2 f ′(x)=−(1+x)^2 +2(1+x)(1−x) =−(1+x)(1+x+2x−2) =−3(1+x)(x−(1/3)) f ′(x)=0 at x=−1, (1/3) Since f(−1)=0, f ′(−1)=0, f(0)=1,f ′(0)=1, f ′((1/3))=0, f((1/3))=((32)/(27)) , f(1)=0 , so for 0≤x≤1, max[f(x)]=((32)/(27)) 4v ≤ ((32)/(27)) ⇒ v=a(b^2 +c)+b(a^2 +c)≤(8/(27)) .](https://www.tinkutara.com/question/Q15246.png)
$$\:\:\:\boldsymbol{{v}}=\boldsymbol{{ab}}^{\mathrm{2}} +\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{b}}+\boldsymbol{{ac}}+\boldsymbol{{bc}} \\ $$$$\:\:\:\boldsymbol{{v}}\:=\boldsymbol{{ab}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)+\boldsymbol{{c}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right) \\ $$$$\:\:\:\:\:\:=\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\left(\boldsymbol{{ab}}+\boldsymbol{{c}}\right)\leqslant\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)\left[\frac{\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right)^{\mathrm{2}} }{\mathrm{4}}+\boldsymbol{{c}}\right] \\ $$$$\:\:\mathrm{4}\boldsymbol{{v}}\:\leqslant\left(\mathrm{1}−\boldsymbol{{c}}\right)\left[\left(\mathrm{1}−\boldsymbol{{c}}\right)^{\mathrm{2}} +\mathrm{4}\boldsymbol{{c}}\right] \\ $$$$\:\:\mathrm{4}\boldsymbol{{v}}\leqslant\left(\mathrm{1}−\boldsymbol{{c}}\right)\left(\mathrm{1}+\boldsymbol{{c}}\right)^{\mathrm{2}} \:\:\:\:\:\left[={f}\left({x}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\leqslant\boldsymbol{{max}}\left[\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right]\:\:\:{for}\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1} \\ $$$$\:\:\:\:\:\:\forall\:{f}\left({x}\right)=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)=−\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right) \\ $$$$\:\:\:\:=−\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}+\mathrm{2}{x}−\mathrm{2}\right) \\ $$$$\:\:\:\:=−\mathrm{3}\left(\mathrm{1}+{x}\right)\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\:{f}\:'\left({x}\right)=\mathrm{0}\:\:{at}\:{x}=−\mathrm{1},\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${Since} \\ $$$$\:{f}\left(−\mathrm{1}\right)=\mathrm{0},\:{f}\:'\left(−\mathrm{1}\right)=\mathrm{0}, \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1},{f}\:'\left(\mathrm{0}\right)=\mathrm{1},\:{f}\:'\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{0}, \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{32}}{\mathrm{27}}\:,\:{f}\left(\mathrm{1}\right)=\mathrm{0}\:\:, \\ $$$${so}\:{for}\:\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1},\:\boldsymbol{{max}}\left[\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\right]=\frac{\mathrm{32}}{\mathrm{27}} \\ $$$$\:\:\mathrm{4}\boldsymbol{{v}}\:\leqslant\:\frac{\mathrm{32}}{\mathrm{27}}\:\: \\ $$$$\Rightarrow\:\boldsymbol{{v}}=\boldsymbol{{a}}\left(\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}\right)+\boldsymbol{{b}}\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{c}}\right)\leqslant\frac{\mathrm{8}}{\mathrm{27}}\:. \\ $$
Commented by mrW1 last updated on 08/Jun/17
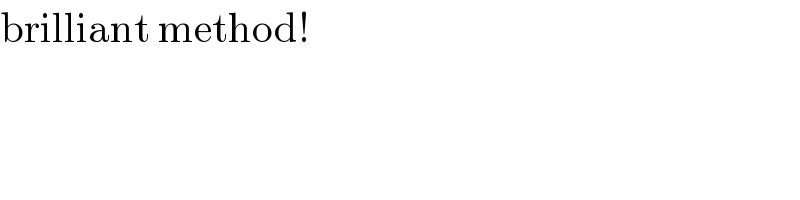
$$\mathrm{brilliant}\:\mathrm{method}! \\ $$
