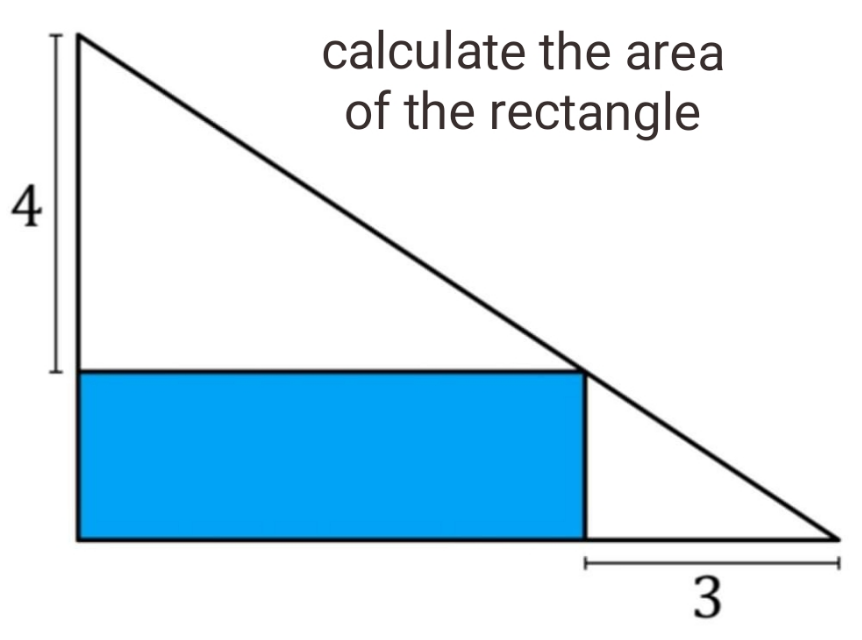
Question Number 152204 by cherokeesay last updated on 26/Aug/21
Commented by Paradoxical last updated on 26/Aug/21
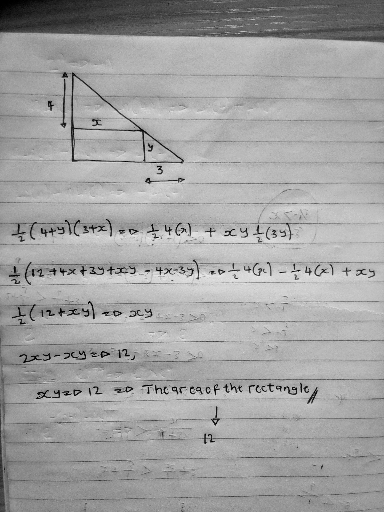
Commented by cherokeesay last updated on 26/Aug/21

$${Nice}\:! \\ $$$${thank}\:{you}\:! \\ $$
Answered by Rasheed.Sindhi last updated on 26/Aug/21

$$\underline{\overline {\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}} \\ $$$${Length}={x}\:,{Width}={y} \\ $$$${Small}\:{trianvles}\:{are}\:{similar}: \\ $$$$\left(\because\:\sphericalangle{s}\:{are}\:{congruent}\right) \\ $$$$\therefore\:\:\frac{{x}}{\mathrm{3}}=\frac{\mathrm{4}}{{y}}\Rightarrow{xy}=\mathrm{12}\Rightarrow{A}=\mathrm{12}\:\mathrm{sq}\:\mathrm{units}. \\ $$$$\:\:\underline{\overline {\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}} \\ $$
Commented by cherokeesay last updated on 26/Aug/21

$${very}\:{clever}\:! \\ $$$${thank}\:{you}\:! \\ $$
Answered by Paradoxical last updated on 26/Aug/21
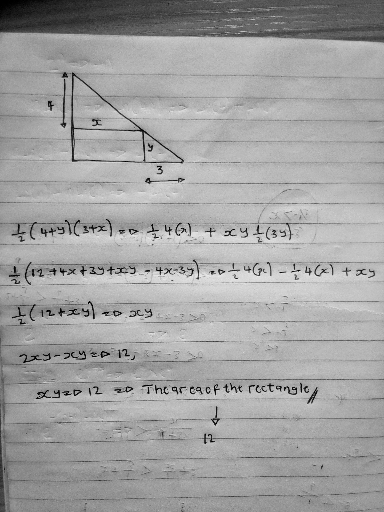
Commented by Rasheed.Sindhi last updated on 27/Aug/21
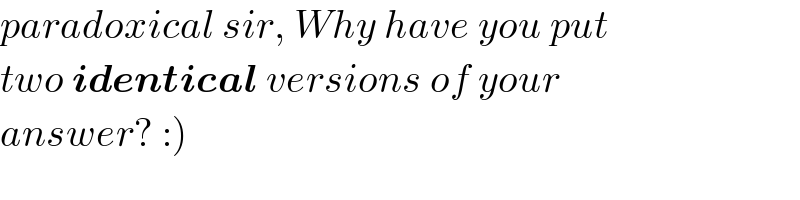
$${paradoxical}\:{sir},\:{Why}\:{have}\:{you}\:{put} \\ $$$${two}\:\boldsymbol{{identical}}\:{versions}\:{of}\:{your} \\ $$$$\left.{answer}?\::\right) \\ $$
Answered by Rasheed.Sindhi last updated on 27/Aug/21

$$\langle\langle\mathcal{T}{hrough}\:\mathcal{H}{ypotenuses}\rangle\rangle \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{Hypotenuses}\:\mathrm{of}\:\mathrm{small}\:\mathrm{triangles} \\ $$$$\:\:\:\:\:\:=\mathrm{Hypotenuse}\:\mathrm{of}\:\mathrm{big}\:\mathrm{triangle} \\ $$$${Length}={x},{Width}={y} \\ $$$$\sqrt{\mathrm{4}^{\mathrm{2}} +{x}^{\mathrm{2}} }+\sqrt{{y}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\sqrt{\left(\mathrm{4}+{y}\right)^{\mathrm{2}} +\left({x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$\mathrm{16}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{9}+\mathrm{2}\sqrt{\mathrm{4}^{\mathrm{2}} +{x}^{\mathrm{2}} }\sqrt{{y}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{16}+\mathrm{8}{y}+{y}^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{6}{x}+\mathrm{9} \\ $$$$\mathrm{2}\sqrt{\mathrm{4}^{\mathrm{2}} +{x}^{\mathrm{2}} }\sqrt{{y}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\mathrm{8}{y}+\mathrm{6}{x} \\ $$$$\sqrt{\mathrm{4}^{\mathrm{2}} +{x}^{\mathrm{2}} }\sqrt{{y}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }=\mathrm{4}{y}+\mathrm{3}{x} \\ $$$$\left(\mathrm{16}+{x}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} +\mathrm{9}\right)=\mathrm{16}{y}^{\mathrm{2}} +\mathrm{24}{xy}+\mathrm{9}{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{9}{x}^{\mathrm{2}} +\mathrm{16}{y}^{\mathrm{2}} +\mathrm{144}=\mathrm{16}{y}^{\mathrm{2}} +\mathrm{24}{xy}+\mathrm{9}{x}^{\mathrm{2}} \\ $$$$\left({xy}\right)^{\mathrm{2}} −\mathrm{24}\left({xy}\right)+\mathrm{144}=\mathrm{0} \\ $$$$\left({xy}−\mathrm{12}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${xy}=\mathrm{12} \\ $$
