Menu Close

Question-152310

Tinku Tara 0 Comments
Pin




Question Number 152310 by DELETED last updated on 27/Aug/21
Answered by DELETED last updated on 27/Aug/21
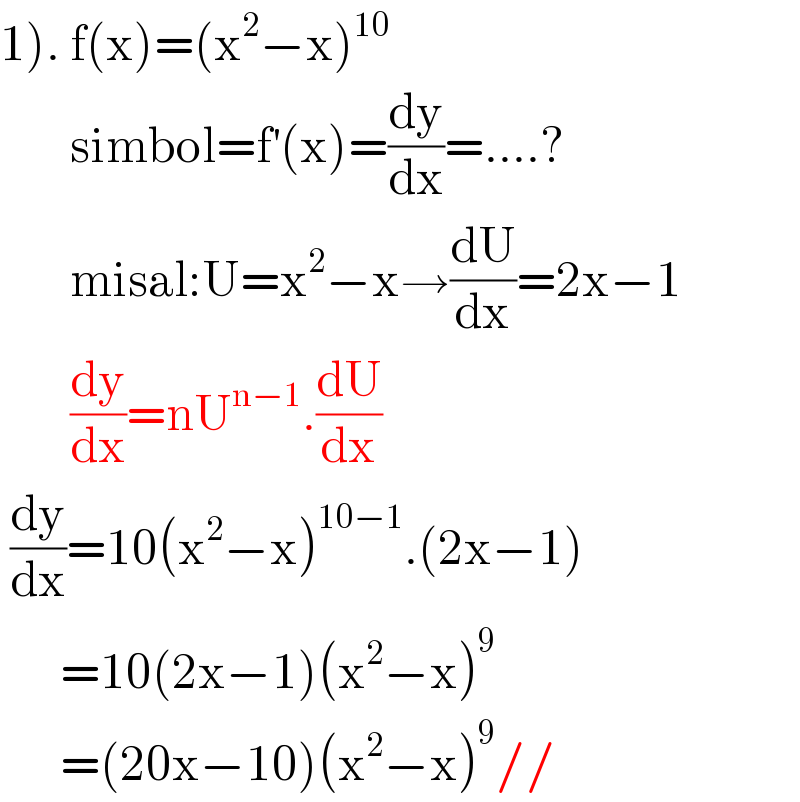
1). f(x)=(x^2 −x)^(10) simbol=f^′ (x)=(dy/dx)=....? misal:U=x^2 −x→(dU/dx)=2x−1 (dy/dx)=nU^(n−1) .(dU/dx) (dy/dx)=10(x^2 −x)^(10−1) .(2x−1) =10(2x−1)(x^2 −x)^9 =(20x−10)(x^2 −x)^9 //
$$\left.\mathrm{1}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)^{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:\mathrm{simbol}=\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{dy}}{\mathrm{dx}}=….? \\ $$$$\:\:\:\:\:\:\:\mathrm{misal}:\mathrm{U}=\mathrm{x}^{\mathrm{2}} −\mathrm{x}\rightarrow\frac{\mathrm{dU}}{\mathrm{dx}}=\mathrm{2x}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{nU}^{\mathrm{n}−\mathrm{1}} .\frac{\mathrm{dU}}{\mathrm{dx}} \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{10}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)^{\mathrm{10}−\mathrm{1}} .\left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:=\mathrm{10}\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)^{\mathrm{9}} \\ $$$$\:\:\:\:\:\:=\left(\mathrm{20x}−\mathrm{10}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right)^{\mathrm{9}} // \\ $$
Answered by DELETED last updated on 27/Aug/21
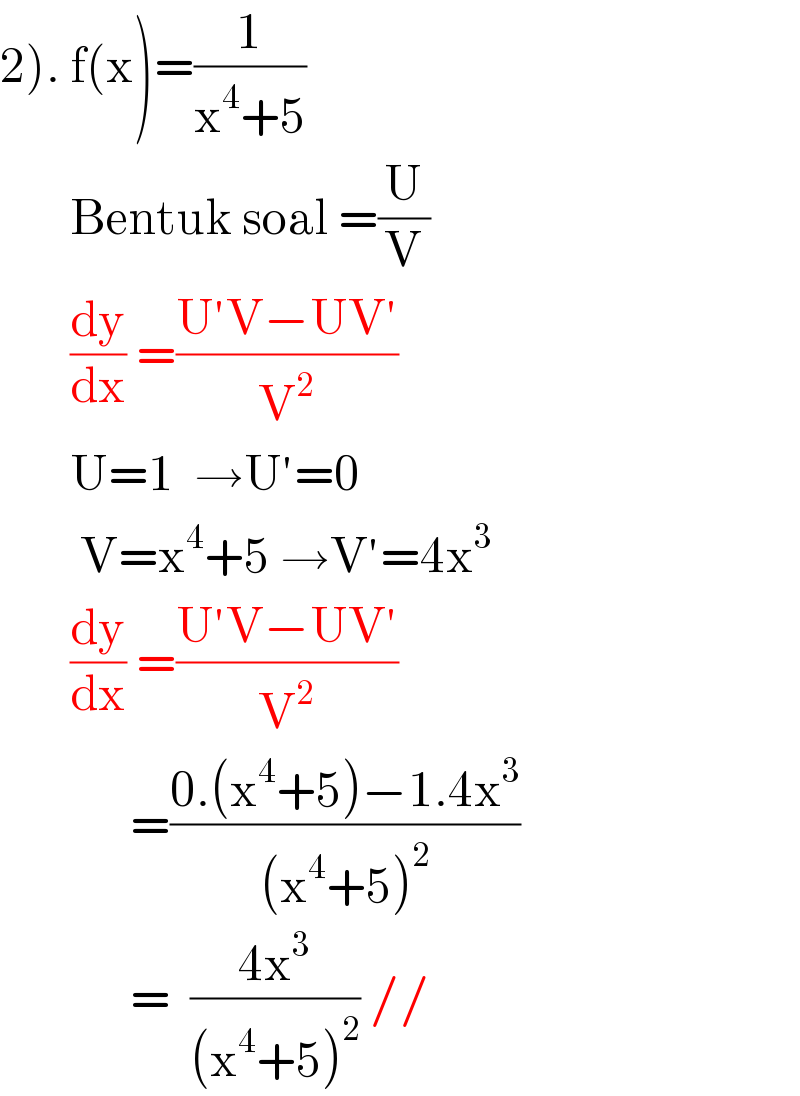
2). f(x)=(1/(x^4 +5)) Bentuk soal =(U/V) (dy/dx) =((U′V−UV′)/V^2 ) U=1 →U′=0 V=x^4 +5 →V′=4x^3 (dy/dx) =((U′V−UV′)/V^2 ) =((0.(x^4 +5)−1.4x^3 )/((x^4 +5)^2 )) = ((4x^3 )/((x^4 +5)^2 )) //
$$\left.\mathrm{2}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{5}}\: \\ $$$$\:\:\:\:\:\:\:\mathrm{Bentuk}\:\mathrm{soal}\:=\frac{\mathrm{U}}{\mathrm{V}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{U}'\mathrm{V}−\mathrm{UV}'}{\mathrm{V}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\mathrm{U}=\mathrm{1}\:\:\rightarrow\mathrm{U}'=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{V}=\mathrm{x}^{\mathrm{4}} +\mathrm{5}\:\rightarrow\mathrm{V}'=\mathrm{4x}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{U}'\mathrm{V}−\mathrm{UV}'}{\mathrm{V}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{0}.\left(\mathrm{x}^{\mathrm{4}} +\mathrm{5}\right)−\mathrm{1}.\mathrm{4x}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{5}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{4x}^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{5}\right)^{\mathrm{2}} }\:// \\ $$
Answered by DELETED last updated on 27/Aug/21
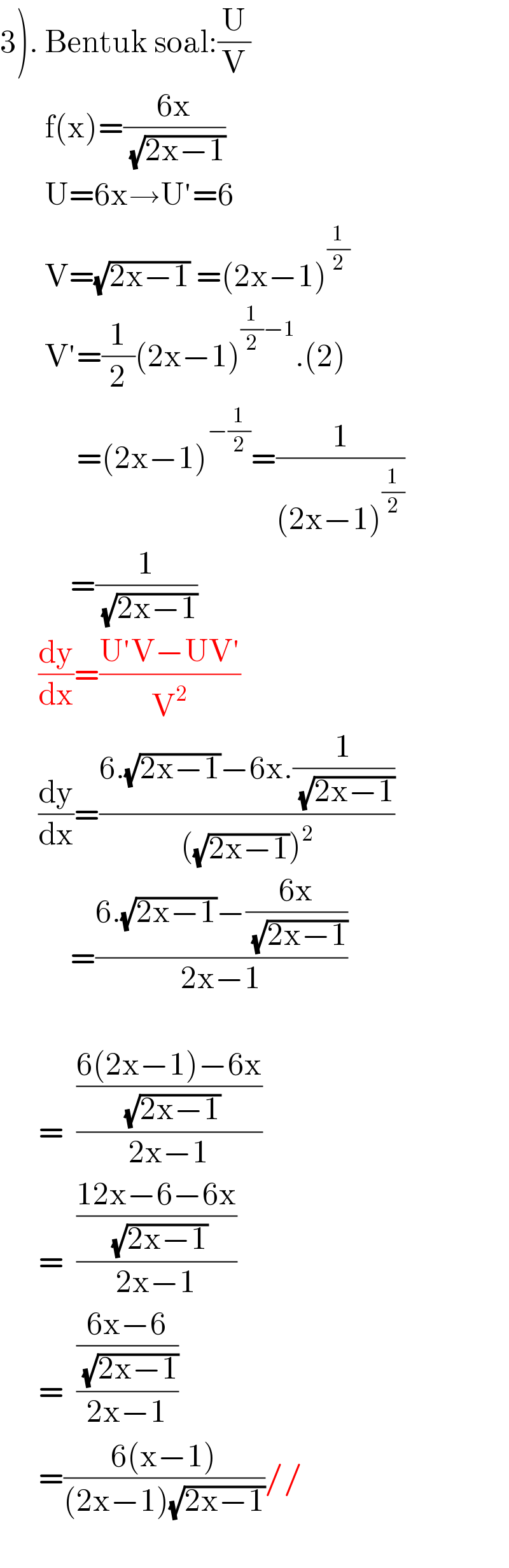
3). Bentuk soal:(U/V) f(x)=((6x)/( (√(2x−1)))) U=6x→U′=6 V=(√(2x−1)) =(2x−1)^(1/2) V′=(1/2)(2x−1)^((1/2)−1) .(2) =(2x−1)^(−(1/2)) =(1/((2x−1)^(1/2) )) =(1/( (√(2x−1)))) (dy/dx)=((U′V−UV′)/V^2 ) (dy/dx)=((6.(√(2x−1))−6x.(1/( (√(2x−1)))))/(((√(2x−1)))^2 )) =((6.(√(2x−1))−((6x)/( (√(2x−1)))))/(2x−1)) = (((6(2x−1)−6x)/( (√(2x−1))))/(2x−1)) = (((12x−6−6x)/( (√(2x−1))))/(2x−1)) = (((6x−6)/( (√(2x−1))))/(2x−1)) =((6(x−1))/((2x−1)(√(2x−1))))//
$$\left.\mathrm{3}\right).\:\mathrm{Bentuk}\:\mathrm{soal}:\frac{\mathrm{U}}{\mathrm{V}} \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{6x}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}} \\ $$$$\:\:\:\:\:\:\:\mathrm{U}=\mathrm{6x}\rightarrow\mathrm{U}'=\mathrm{6} \\ $$$$\:\:\:\:\:\:\:\mathrm{V}=\sqrt{\mathrm{2x}−\mathrm{1}}\:=\left(\mathrm{2x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\mathrm{V}'=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} .\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2x}−\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\left(\mathrm{2x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}\: \\ $$$$\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{U}'\mathrm{V}−\mathrm{UV}'}{\mathrm{V}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{6}.\sqrt{\mathrm{2x}−\mathrm{1}}−\mathrm{6x}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}}{\left(\sqrt{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{6}.\sqrt{\mathrm{2x}−\mathrm{1}}−\frac{\mathrm{6x}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}}{\mathrm{2x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:=\:\:\frac{\frac{\mathrm{6}\left(\mathrm{2x}−\mathrm{1}\right)−\mathrm{6x}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}}{\mathrm{2x}−\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:=\:\:\frac{\frac{\mathrm{12x}−\mathrm{6}−\mathrm{6x}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}}{\mathrm{2x}−\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:=\:\:\frac{\frac{\mathrm{6x}−\mathrm{6}}{\:\sqrt{\mathrm{2x}−\mathrm{1}}}}{\mathrm{2x}−\mathrm{1}}\: \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{6}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{2x}−\mathrm{1}\right)\sqrt{\mathrm{2x}−\mathrm{1}}}// \\ $$$$\:\:\:\:\: \\ $$
Answered by DELETED last updated on 27/Aug/21
4). f(x)=(√((x+2)/(x−1))) =[((x+2)/(x−1))]^(1/2) (dy/dx)=n[(U/V)]^(n−1) .(((U′V−UV′)/V^2 )) (dy/dx)=n[(U/V)]^(n−1) .(((U′V−UV′)/V^2 )) U=2x+2 →U′=2 V=x−1→V′=1 (dy/dx)=(1/2)[((2x+2)/(x−1))]^((1/2)−1) .(((2.(x−1)−(2x+2).1)/((x−1)^2 ))) (dy/dx)=(1/2)[((2x+2)/(x−1))]^(−(1/2)) .(((2x−2−2x−2))/((x−1)^2 ))) (dy/dx)=(1/2)[((x−1)/(2x+2))]^(1/2) .(((−4)/((x−1)^2 ))) (dy/dx)=[((x−1)/(2x+2))]^(1/2) .(((−2)/((x−1)^2 ))) (dy/dx)=[((x−1)/(2x+2))]^(1/2) (((−2)/((x−1)^2 )))=−(2/((2x+2)^(1/2) (x−1)^(3/2) )) =−(2/((x−1)(√((2x+2)(x−1))))) //
$$\left.\mathrm{4}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\sqrt{\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}}\:=\left[\frac{\mathrm{x}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{n}\left[\frac{\mathrm{U}}{\mathrm{V}}\right]^{\mathrm{n}−\mathrm{1}} \:.\left(\frac{\mathrm{U}'\mathrm{V}−\mathrm{UV}'}{\mathrm{V}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{n}\left[\frac{\mathrm{U}}{\mathrm{V}}\right]^{\mathrm{n}−\mathrm{1}} \:.\left(\frac{\mathrm{U}'\mathrm{V}−\mathrm{UV}'}{\mathrm{V}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\mathrm{U}=\mathrm{2x}+\mathrm{2}\:\rightarrow\mathrm{U}'=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\mathrm{V}=\mathrm{x}−\mathrm{1}\rightarrow\mathrm{V}'=\mathrm{1} \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2x}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:.\left(\frac{\mathrm{2}.\left(\mathrm{x}−\mathrm{1}\right)−\left(\mathrm{2x}+\mathrm{2}\right).\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2x}+\mathrm{2}}{\mathrm{x}−\mathrm{1}}\right]^{−\frac{\mathrm{1}}{\mathrm{2}}} \:.\left(\frac{\left.\mathrm{2x}−\mathrm{2}−\mathrm{2x}−\mathrm{2}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{x}−\mathrm{1}}{\mathrm{2x}+\mathrm{2}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \:.\left(\frac{−\mathrm{4}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\left[\frac{\mathrm{x}−\mathrm{1}}{\mathrm{2x}+\mathrm{2}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \:.\left(\frac{−\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=\left[\frac{\mathrm{x}−\mathrm{1}}{\mathrm{2x}+\mathrm{2}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\frac{−\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right)=−\frac{\mathrm{2}}{\left(\mathrm{2x}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=−\frac{\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)\sqrt{\left(\mathrm{2x}+\mathrm{2}\right)\left(\mathrm{x}−\mathrm{1}\right)}}\:// \\ $$$$\:\:\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *