Question Number 152407 by imjagoll last updated on 28/Aug/21
Answered by Olaf_Thorendsen last updated on 28/Aug/21

$${f}\left({x},{y}\right)\:=\:\frac{\left({x}+{y}\right)\mathrm{sec}\left({x}+{y}\right)−{x}\mathrm{sec}{x}}{{y}} \\ $$$${f}\left({x},{y}\right)\:=\:\frac{\frac{{x}+{y}}{\mathrm{cos}\left({x}+{y}\right)}−{x}\mathrm{sec}{x}}{{y}} \\ $$$${f}\left({x},{y}\right)\:=\:\frac{\frac{{x}+{y}}{\mathrm{cos}{x}\mathrm{cos}{y}−\mathrm{sin}{x}\mathrm{sin}{y}}−{x}\mathrm{sec}{x}}{{y}} \\ $$$${f}\left({x},{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:\frac{\frac{{x}+{y}}{\mathrm{cos}{x}−{y}\mathrm{sin}{x}}−{x}\mathrm{sec}{x}}{{y}} \\ $$$${f}\left({x},{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:\frac{\frac{{x}+{y}}{\mathrm{1}−{y}\mathrm{tan}{x}}−{x}}{{y}\mathrm{cos}{x}} \\ $$$${f}\left({x},{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:\frac{\left({x}+{y}\right)\left(\mathrm{1}+{y}\mathrm{tan}{x}\right)−{x}}{{y}\mathrm{cos}{x}} \\ $$$${f}\left({x},{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:\frac{{x}+{y}\left(\mathrm{1}+{x}\mathrm{tan}{x}\right)−{x}}{{y}\mathrm{cos}{x}} \\ $$$${f}\left({x},{y}\right)\:\underset{{y}\rightarrow\mathrm{0}} {\sim}\:\frac{\mathrm{1}+{x}\mathrm{tan}{x}}{\mathrm{cos}{x}} \\ $$
Answered by EDWIN88 last updated on 28/Aug/21
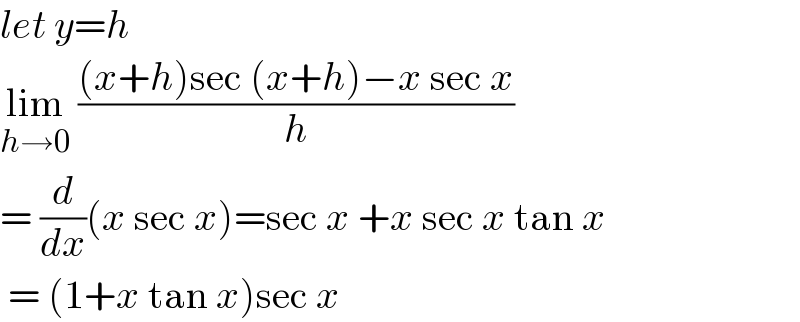
$${let}\:{y}={h}\: \\ $$$$\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({x}+{h}\right)\mathrm{sec}\:\left({x}+{h}\right)−{x}\:\mathrm{sec}\:{x}}{{h}}\: \\ $$$$=\:\frac{{d}}{{dx}}\left({x}\:\mathrm{sec}\:{x}\right)=\mathrm{sec}\:{x}\:+{x}\:\mathrm{sec}\:{x}\:\mathrm{tan}\:{x} \\ $$$$\:=\:\left(\mathrm{1}+{x}\:\mathrm{tan}\:{x}\right)\mathrm{sec}\:{x} \\ $$
