Question Number 152441 by fotosy2k last updated on 28/Aug/21

Commented by fotosy2k last updated on 28/Aug/21

$${pls}\:{help} \\ $$
Answered by qaz last updated on 28/Aug/21
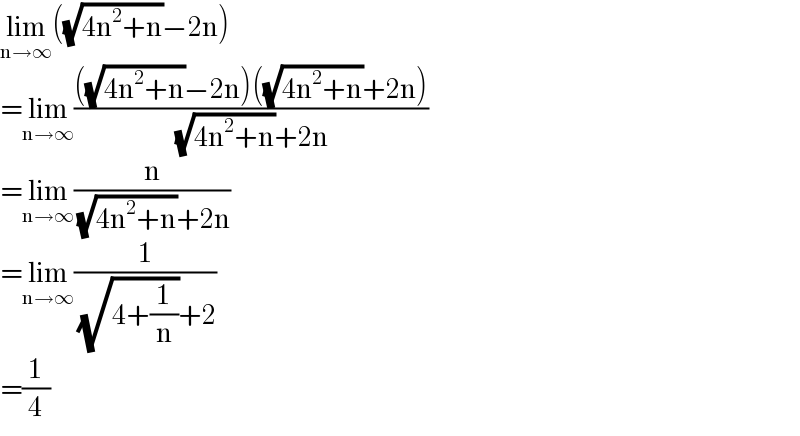
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{n}}−\mathrm{2n}\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{n}}−\mathrm{2n}\right)\left(\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{n}}+\mathrm{2n}\right)}{\:\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{n}}+\mathrm{2n}} \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{n}}{\:\sqrt{\mathrm{4n}^{\mathrm{2}} +\mathrm{n}}+\mathrm{2n}} \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}+\frac{\mathrm{1}}{\mathrm{n}}}+\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by fotosy2k last updated on 30/Aug/21

$${thank}\:{you} \\ $$
Answered by puissant last updated on 28/Aug/21

$$={lim}_{{n}\rightarrow\infty} \frac{\mathrm{4}{n}^{\mathrm{2}} +{n}−\mathrm{4}{n}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{n}^{\mathrm{2}} +{n}}+\mathrm{2}{n}}\: \\ $$$$={lim}_{{n}\rightarrow\infty} \frac{{n}}{{n}\left(\sqrt{\mathrm{4}+\frac{\mathrm{1}}{{n}}}+\mathrm{2}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left.\:\:\:\:\:\:{B}\right) \\ $$
Commented by fotosy2k last updated on 30/Aug/21

$${thank}\:{you} \\ $$
Answered by EDWIN88 last updated on 28/Aug/21

$$\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}{n}^{\mathrm{2}} +{n}}−\mathrm{2}{n}\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}2}\left({n}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{4}}\right)−\mathrm{2}{n} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by fotosy2k last updated on 30/Aug/21

$${thank}\:{you} \\ $$
