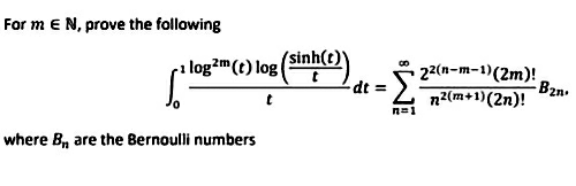
Question Number 152464 by mathdanisur last updated on 28/Aug/21
Answered by mindispower last updated on 29/Aug/21
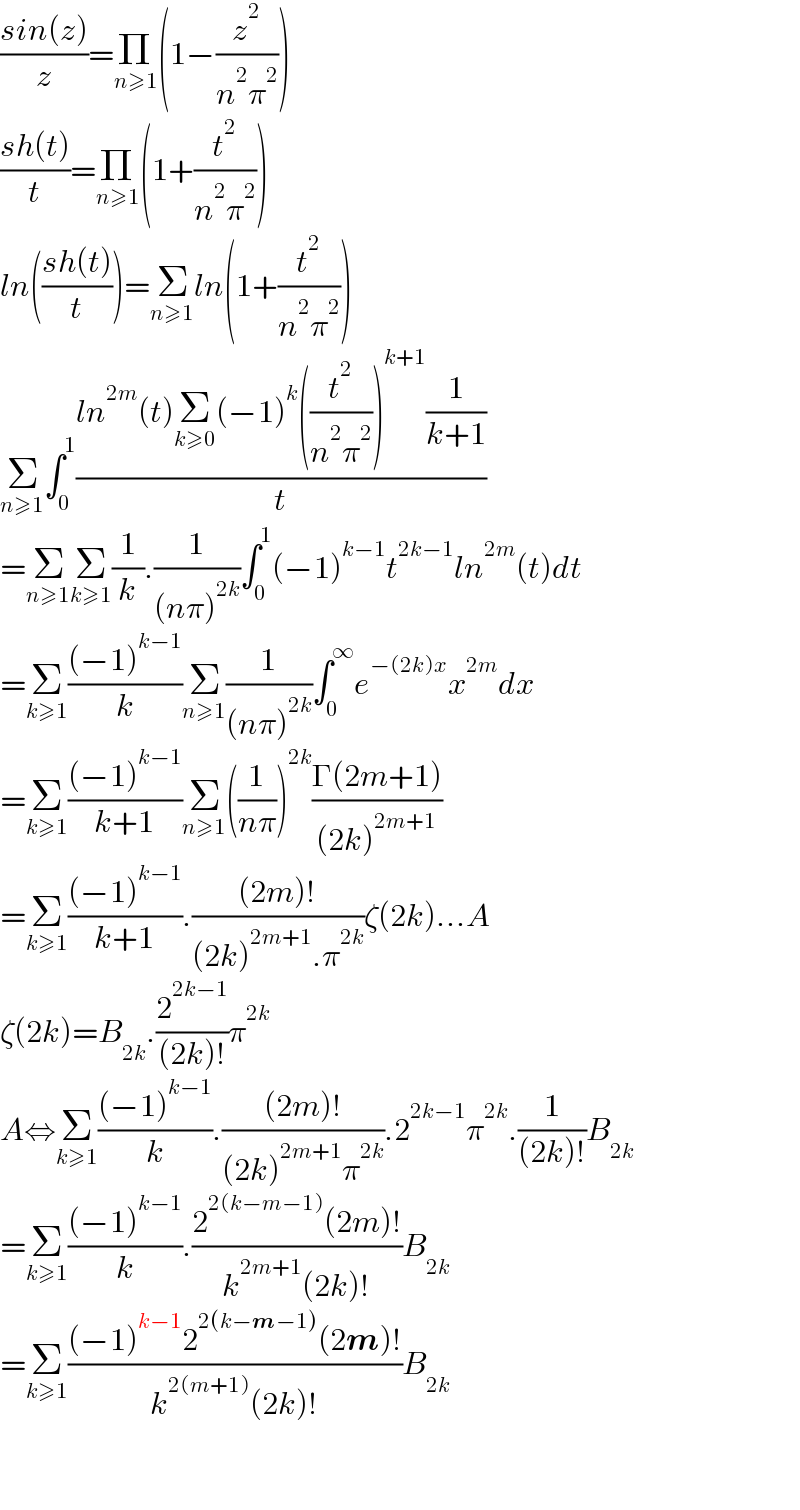
$$\frac{{sin}\left({z}\right)}{{z}}=\underset{{n}\geqslant\mathrm{1}} {\prod}\left(\mathrm{1}−\frac{{z}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$$\frac{{sh}\left({t}\right)}{{t}}=\underset{{n}\geqslant\mathrm{1}} {\prod}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$${ln}\left(\frac{{sh}\left({t}\right)}{{t}}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}{ln}\left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}{m}} \left({t}\right)\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} \left(\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} \pi^{\mathrm{2}} }\right)^{{k}+\mathrm{1}} \frac{\mathrm{1}}{{k}+\mathrm{1}}}{{t}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{k}}.\frac{\mathrm{1}}{\left({n}\pi\right)^{\mathrm{2}{k}} }\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{k}−\mathrm{1}} {t}^{\mathrm{2}{k}−\mathrm{1}} {ln}^{\mathrm{2}{m}} \left({t}\right){dt} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}\pi\right)^{\mathrm{2}{k}} }\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{2}{k}\right){x}} {x}^{\mathrm{2}{m}} {dx} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}+\mathrm{1}}\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}\pi}\right)^{\mathrm{2}{k}} \frac{\Gamma\left(\mathrm{2}{m}+\mathrm{1}\right)}{\left(\mathrm{2}{k}\right)^{\mathrm{2}{m}+\mathrm{1}} } \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}+\mathrm{1}}.\frac{\left(\mathrm{2}{m}\right)!}{\left(\mathrm{2}{k}\right)^{\mathrm{2}{m}+\mathrm{1}} .\pi^{\mathrm{2}{k}} }\zeta\left(\mathrm{2}{k}\right)…{A} \\ $$$$\zeta\left(\mathrm{2}{k}\right)={B}_{\mathrm{2}{k}} .\frac{\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} }{\left(\mathrm{2}{k}\right)!}\pi^{\mathrm{2}{k}} \\ $$$${A}\Leftrightarrow\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}.\frac{\left(\mathrm{2}{m}\right)!}{\left(\mathrm{2}{k}\right)^{\mathrm{2}{m}+\mathrm{1}} \pi^{\mathrm{2}{k}} }.\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} \pi^{\mathrm{2}{k}} .\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)!}{B}_{\mathrm{2}{k}} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}.\frac{\mathrm{2}^{\mathrm{2}\left({k}−{m}−\mathrm{1}\right)} \left(\mathrm{2}{m}\right)!}{{k}^{\mathrm{2}{m}+\mathrm{1}} \left(\mathrm{2}{k}\right)!}{B}_{\mathrm{2}{k}} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} \mathrm{2}^{\mathrm{2}\left({k}−\boldsymbol{{m}}−\mathrm{1}\right)} \left(\mathrm{2}\boldsymbol{{m}}\right)!}{{k}^{\mathrm{2}\left({m}+\mathrm{1}\right)} \left(\mathrm{2}{k}\right)!}{B}_{\mathrm{2}{k}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathdanisur last updated on 29/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
