Menu Close

Question-152478

Tinku Tara 0 Comments
Pin




Question Number 152478 by imjagoll last updated on 28/Aug/21
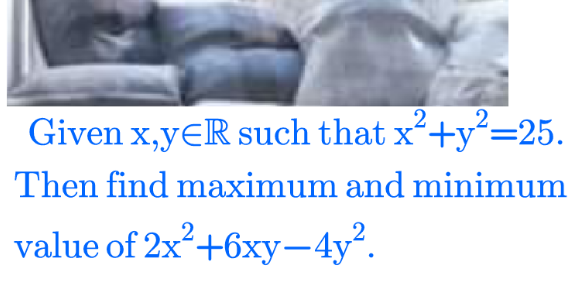
Answered by mr W last updated on 28/Aug/21
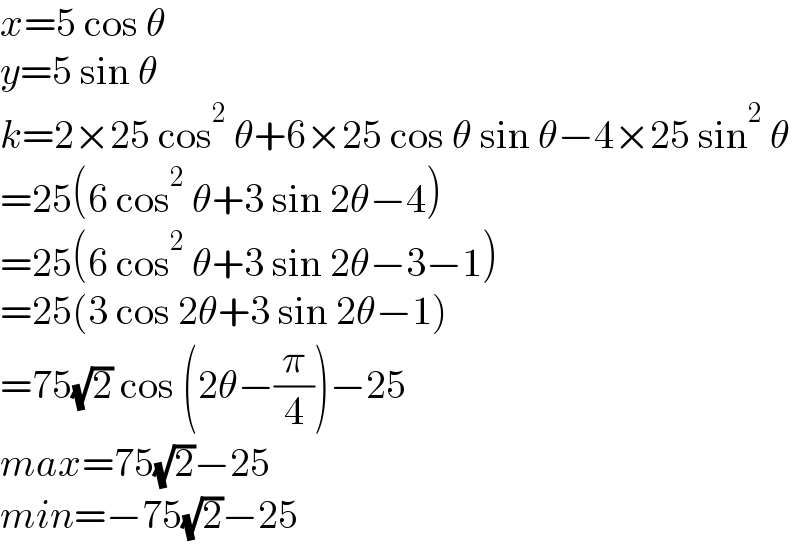
x=5 cos θ y=5 sin θ k=2×25 cos^2 θ+6×25 cos θ sin θ−4×25 sin^2 θ =25(6 cos^2 θ+3 sin 2θ−4) =25(6 cos^2 θ+3 sin 2θ−3−1) =25(3 cos 2θ+3 sin 2θ−1) =75(√2) cos (2θ−(π/4))−25 max=75(√2)−25 min=−75(√2)−25
$${x}=\mathrm{5}\:\mathrm{cos}\:\theta \\ $$$${y}=\mathrm{5}\:\mathrm{sin}\:\theta \\ $$$${k}=\mathrm{2}×\mathrm{25}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{6}×\mathrm{25}\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta−\mathrm{4}×\mathrm{25}\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$=\mathrm{25}\left(\mathrm{6}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\theta−\mathrm{4}\right) \\ $$$$=\mathrm{25}\left(\mathrm{6}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\theta−\mathrm{3}−\mathrm{1}\right) \\ $$$$=\mathrm{25}\left(\mathrm{3}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\theta−\mathrm{1}\right) \\ $$$$=\mathrm{75}\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\mathrm{2}\theta−\frac{\pi}{\mathrm{4}}\right)−\mathrm{25} \\ $$$${max}=\mathrm{75}\sqrt{\mathrm{2}}−\mathrm{25} \\ $$$${min}=−\mathrm{75}\sqrt{\mathrm{2}}−\mathrm{25} \\ $$
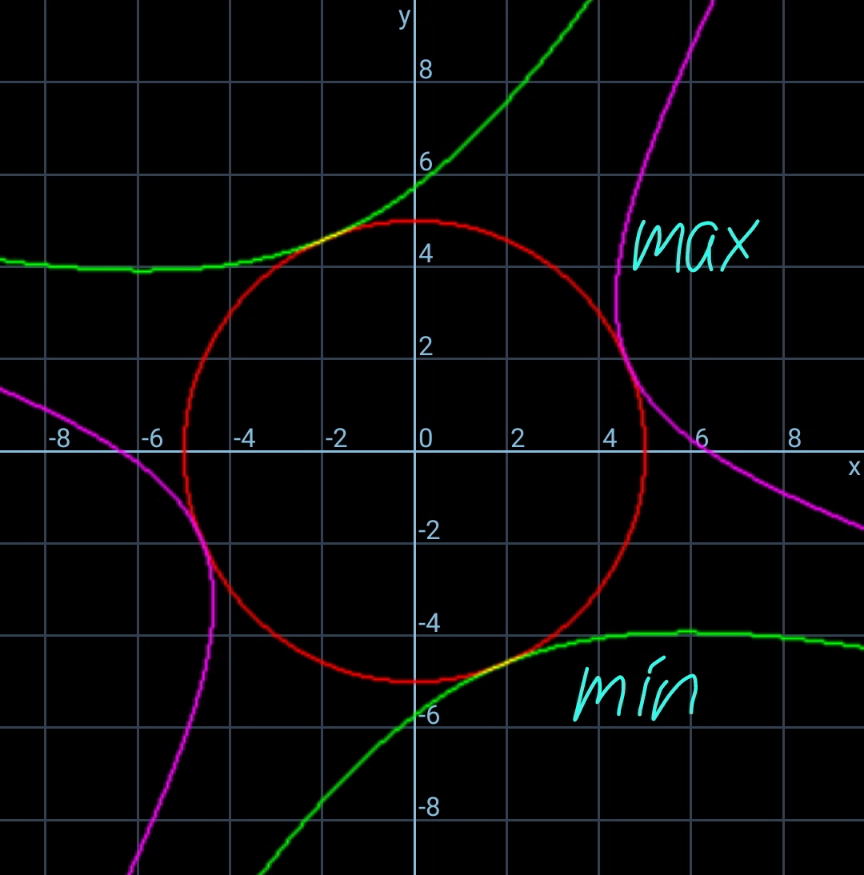
Commented by mr W last updated on 28/Aug/21
Answered by bramlexs22 last updated on 29/Aug/21
f(x,y)= 2(x^2 +y^2 )+6xy−6y^2 =6xy−6y^2 +50 where y=(√(25−x^2 )) f(x)=6x(√(25−x^2 ))−6(25−x^2 )+50 f(x)=6x(√(25−x^2 ))+6x^2 −100 ((df(x))/dx) = 6(√(25−x^2 ))−((6x^2 )/( (√(25−x^2 ))))+12x=0 ⇒(√(25−x^2 ))+2x =(x^2 /( (√(25−x^2 )))) ⇒25−x^2 +2x(√(25−x^2 )) =x^2 ⇒2x^2 −25=2x(√(25−x^2 )) ⇒4x^4 −100x^2 +625=4x^2 (25−x^2 ) ⇒8x^4 −200x^2 +625=0 ⇒x^2 =((200 + (√(200^2 −32×625)))/(16)) = ((200+100(√2))/(16)) ⇒x^2 =((50+25(√2))/4) then y^2 =25−(((50+25(√2))/4))=((50−25(√2))/4) ⇒x^2 y^2 =(((50+25(√2))/4))(((50−25(√2))/4))=((1250)/(16)) ⇒xy=(√((1250)/(16)))=±((25(√2))/4) max (2x^2 +6xy−4y^2 )=6(((25(√2))/4))−6(((50−25(√2))/4))+50 =((150(√2)−300+150(√2)+200)/4) =75(√2)−25 min (2x^2 +6xy−4y^2 )=−6(((25(√2))/4))−6(((50−25(√2))/4))+50 =((−150(√2)−300+150(√2)+200)/4)
$$\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\:\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)+\mathrm{6xy}−\mathrm{6y}^{\mathrm{2}} =\mathrm{6xy}−\mathrm{6y}^{\mathrm{2}} +\mathrm{50} \\ $$$$\mathrm{where}\:\mathrm{y}=\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{6x}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }−\mathrm{6}\left(\mathrm{25}−\mathrm{x}^{\mathrm{2}} \right)+\mathrm{50} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{6x}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }+\mathrm{6x}^{\mathrm{2}} −\mathrm{100} \\ $$$$\frac{\mathrm{df}\left(\mathrm{x}\right)}{\mathrm{dx}}\:=\:\mathrm{6}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{6x}^{\mathrm{2}} }{\:\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }}+\mathrm{12x}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }+\mathrm{2x}\:=\frac{\mathrm{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{25}−\mathrm{x}^{\mathrm{2}} +\mathrm{2x}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} }\:=\mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2x}^{\mathrm{2}} −\mathrm{25}=\mathrm{2x}\sqrt{\mathrm{25}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{4x}^{\mathrm{4}} −\mathrm{100x}^{\mathrm{2}} +\mathrm{625}=\mathrm{4x}^{\mathrm{2}} \left(\mathrm{25}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{8x}^{\mathrm{4}} −\mathrm{200x}^{\mathrm{2}} +\mathrm{625}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{200}\:+\:\sqrt{\mathrm{200}^{\mathrm{2}} −\mathrm{32}×\mathrm{625}}}{\mathrm{16}}\:=\:\frac{\mathrm{200}+\mathrm{100}\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{50}+\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\mathrm{then}\:\mathrm{y}^{\mathrm{2}} =\mathrm{25}−\left(\frac{\mathrm{50}+\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)=\frac{\mathrm{50}−\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} =\left(\frac{\mathrm{50}+\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)\left(\frac{\mathrm{50}−\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)=\frac{\mathrm{1250}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{xy}=\sqrt{\frac{\mathrm{1250}}{\mathrm{16}}}=\pm\frac{\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\mathrm{max}\:\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{6xy}−\mathrm{4y}^{\mathrm{2}} \right)=\mathrm{6}\left(\frac{\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{6}\left(\frac{\mathrm{50}−\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)+\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{150}\sqrt{\mathrm{2}}−\mathrm{300}+\mathrm{150}\sqrt{\mathrm{2}}+\mathrm{200}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{75}\sqrt{\mathrm{2}}−\mathrm{25} \\ $$$$\mathrm{min}\:\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{6xy}−\mathrm{4y}^{\mathrm{2}} \right)=−\mathrm{6}\left(\frac{\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)−\mathrm{6}\left(\frac{\mathrm{50}−\mathrm{25}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)+\mathrm{50} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{150}\sqrt{\mathrm{2}}−\mathrm{300}+\mathrm{150}\sqrt{\mathrm{2}}+\mathrm{200}}{\mathrm{4}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *