Menu Close

Question-152481

Tinku Tara 0 Comments
Pin




Question Number 152481 by mathdanisur last updated on 28/Aug/21
Commented by Rasheed.Sindhi last updated on 29/Aug/21
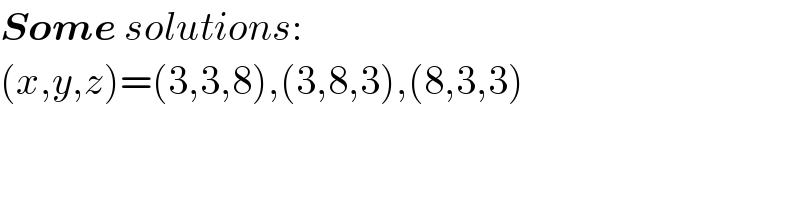
Some solutions: (x,y,z)=(3,3,8),(3,8,3),(8,3,3)
$$\boldsymbol{{Some}}\:{solutions}: \\ $$$$\left({x},{y},{z}\right)=\left(\mathrm{3},\mathrm{3},\mathrm{8}\right),\left(\mathrm{3},\mathrm{8},\mathrm{3}\right),\left(\mathrm{8},\mathrm{3},\mathrm{3}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 29/Aug/21
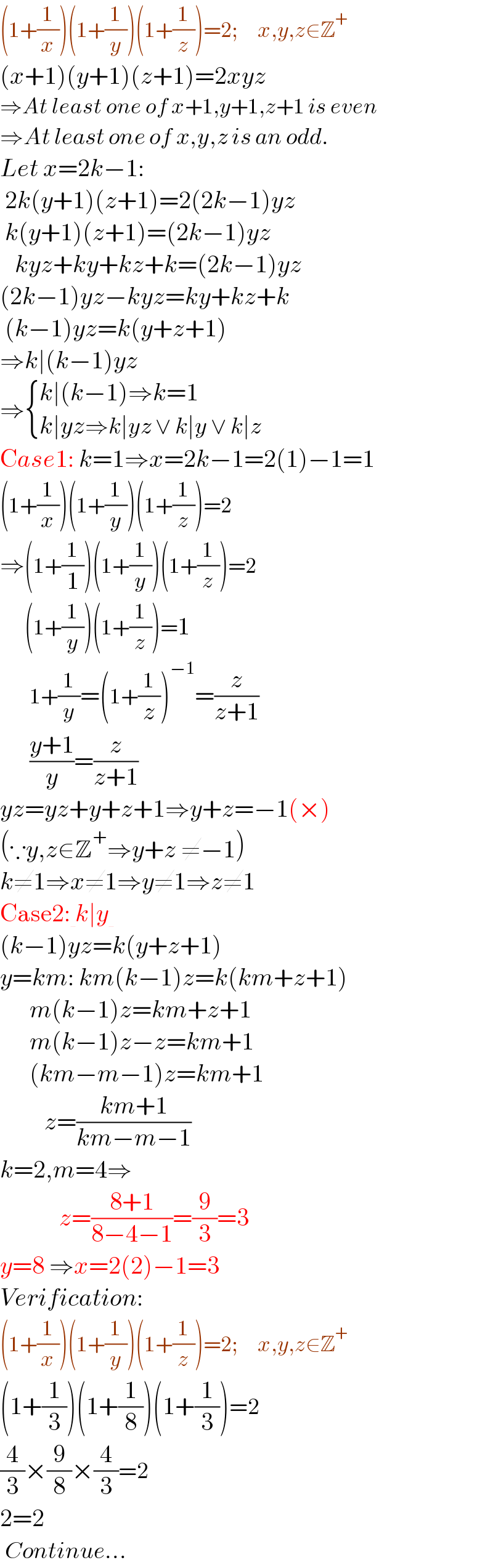
(1+(1/x))(1+(1/y))(1+(1/z))=2; x,y,z∈Z^+ (x+1)(y+1)(z+1)=2xyz ⇒At least one of x+1,y+1,z+1 is even ⇒At least one of x,y,z is an odd. Let x=2k−1: 2k(y+1)(z+1)=2(2k−1)yz k(y+1)(z+1)=(2k−1)yz kyz+ky+kz+k=(2k−1)yz (2k−1)yz−kyz=ky+kz+k (k−1)yz=k(y+z+1) ⇒k∣(k−1)yz ⇒ { ((k∣(k−1)⇒k=1)),((k∣yz⇒k∣yz ∨ k∣y ∨ k∣z)) :} Case1: k=1⇒x=2k−1=2(1)−1=1 (1+(1/x))(1+(1/y))(1+(1/z))=2 ⇒(1+(1/1))(1+(1/y))(1+(1/z))=2 (1+(1/y))(1+(1/z))=1 1+(1/y)=(1+(1/z))^(−1) =(z/(z+1)) ((y+1)/y)=(z/(z+1)) yz=yz+y+z+1⇒y+z=−1(×) (∵y,z∈Z^+ ⇒y+z ≠−1) k≠1⇒x≠1⇒y≠1⇒z≠1 Case2: k∣y (k−1)yz=k(y+z+1) y=km: km(k−1)z=k(km+z+1) m(k−1)z=km+z+1 m(k−1)z−z=km+1 (km−m−1)z=km+1 z=((km+1)/(km−m−1)) k=2,m=4⇒ z=((8+1)/(8−4−1))=(9/3)=3 y=8 ⇒x=2(2)−1=3 Verification: (1+(1/x))(1+(1/y))(1+(1/z))=2; x,y,z∈Z^+ (1+(1/3))(1+(1/8))(1+(1/3))=2 (4/3)×(9/8)×(4/3)=2 2=2 Continue...
$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{2};\:\:\:\:{x},{y},{z}\in\mathbb{Z}^{+} \\ $$$$\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\mathrm{2}{xyz} \\ $$$$\Rightarrow{At}\:{least}\:{one}\:{of}\:{x}+\mathrm{1},{y}+\mathrm{1},{z}+\mathrm{1}\:{is}\:{even} \\ $$$$\Rightarrow{At}\:{least}\:{one}\:{of}\:{x},{y},{z}\:{is}\:{an}\:{odd}. \\ $$$${Let}\:{x}=\mathrm{2}{k}−\mathrm{1}: \\ $$$$\:\mathrm{2}{k}\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\mathrm{2}\left(\mathrm{2}{k}−\mathrm{1}\right){yz} \\ $$$$\:{k}\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\left(\mathrm{2}{k}−\mathrm{1}\right){yz} \\ $$$$\:\:\:{kyz}+{ky}+{kz}+{k}=\left(\mathrm{2}{k}−\mathrm{1}\right){yz} \\ $$$$\left(\mathrm{2}{k}−\mathrm{1}\right){yz}−{kyz}={ky}+{kz}+{k} \\ $$$$\:\left({k}−\mathrm{1}\right){yz}={k}\left({y}+{z}+\mathrm{1}\right) \\ $$$$\Rightarrow{k}\mid\left({k}−\mathrm{1}\right){yz} \\ $$$$\Rightarrow\begin{cases}{{k}\mid\left({k}−\mathrm{1}\right)\Rightarrow{k}=\mathrm{1}}\\{{k}\mid{yz}\Rightarrow{k}\mid{yz}\:\vee\:{k}\mid{y}\:\vee\:{k}\mid{z}}\end{cases} \\ $$$$\mathrm{C}{ase}\mathrm{1}:\:{k}=\mathrm{1}\Rightarrow{x}=\mathrm{2}{k}−\mathrm{1}=\mathrm{2}\left(\mathrm{1}\right)−\mathrm{1}=\mathrm{1} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{2} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{2} \\ $$$$\:\:\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{1}+\frac{\mathrm{1}}{{y}}=\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)^{−\mathrm{1}} =\frac{{z}}{{z}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\frac{{y}+\mathrm{1}}{{y}}=\frac{{z}}{{z}+\mathrm{1}} \\ $$$${yz}={yz}+{y}+{z}+\mathrm{1}\Rightarrow{y}+{z}=−\mathrm{1}\left(×\right) \\ $$$$\left(\because{y},{z}\in\mathbb{Z}^{+} \Rightarrow{y}+{z}\:\neq−\mathrm{1}\right) \\ $$$${k}\neq\mathrm{1}\Rightarrow{x}\neq\mathrm{1}\Rightarrow{y}\neq\mathrm{1}\Rightarrow{z}\neq\mathrm{1} \\ $$$$\mathrm{Case2}:\underline{\:}{k}\mid{y}\underline{\:} \\ $$$$\left({k}−\mathrm{1}\right){yz}={k}\left({y}+{z}+\mathrm{1}\right) \\ $$$${y}={km}:\:{km}\left({k}−\mathrm{1}\right){z}={k}\left({km}+{z}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:{m}\left({k}−\mathrm{1}\right){z}={km}+{z}+\mathrm{1} \\ $$$$\:\:\:\:\:\:{m}\left({k}−\mathrm{1}\right){z}−{z}={km}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\left({km}−{m}−\mathrm{1}\right){z}={km}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:{z}=\frac{{km}+\mathrm{1}}{{km}−{m}−\mathrm{1}} \\ $$$${k}=\mathrm{2},{m}=\mathrm{4}\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{z}=\frac{\mathrm{8}+\mathrm{1}}{\mathrm{8}−\mathrm{4}−\mathrm{1}}=\frac{\mathrm{9}}{\mathrm{3}}=\mathrm{3} \\ $$$${y}=\mathrm{8}\:\Rightarrow{x}=\mathrm{2}\left(\mathrm{2}\right)−\mathrm{1}=\mathrm{3} \\ $$$${Verification}: \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{z}}\right)=\mathrm{2};\:\:\:\:{x},{y},{z}\in\mathbb{Z}^{+} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{2} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{8}}×\frac{\mathrm{4}}{\mathrm{3}}=\mathrm{2} \\ $$$$\mathrm{2}=\mathrm{2} \\ $$$$\:{Continue}…\:\:\:\:\: \\ $$
Commented by mathdanisur last updated on 29/Aug/21
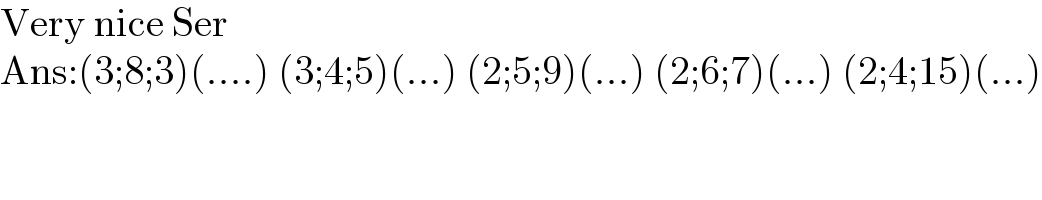
Very nice Ser Ans:(3;8;3)(....) (3;4;5)(...) (2;5;9)(...) (2;6;7)(...) (2;4;15)(...)
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser} \\ $$$$\mathrm{Ans}:\left(\mathrm{3};\mathrm{8};\mathrm{3}\right)\left(….\right)\:\left(\mathrm{3};\mathrm{4};\mathrm{5}\right)\left(…\right)\:\left(\mathrm{2};\mathrm{5};\mathrm{9}\right)\left(…\right)\:\left(\mathrm{2};\mathrm{6};\mathrm{7}\right)\left(…\right)\:\left(\mathrm{2};\mathrm{4};\mathrm{15}\right)\left(…\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *