Question Number 152486 by Tawa11 last updated on 28/Aug/21

Answered by mr W last updated on 29/Aug/21

Commented by mr W last updated on 29/Aug/21
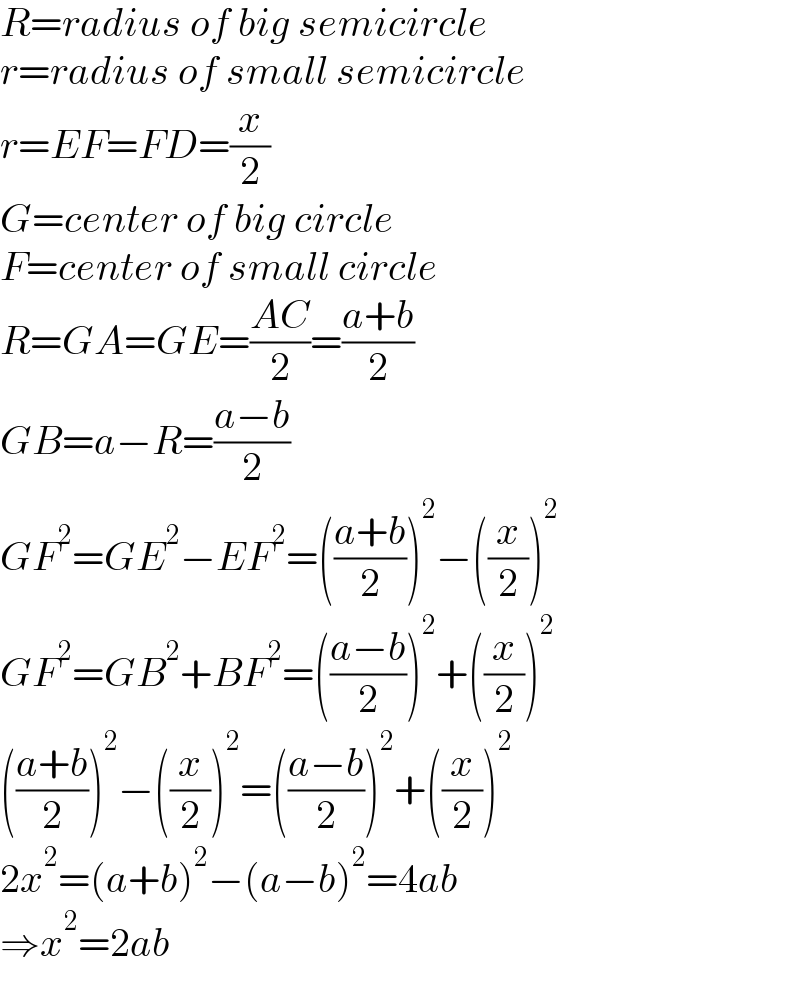
$${R}={radius}\:{of}\:{big}\:{semicircle} \\ $$$${r}={radius}\:{of}\:{small}\:{semicircle} \\ $$$${r}={EF}={FD}=\frac{{x}}{\mathrm{2}} \\ $$$${G}={center}\:{of}\:{big}\:{circle} \\ $$$${F}={center}\:{of}\:{small}\:{circle} \\ $$$${R}={GA}={GE}=\frac{{AC}}{\mathrm{2}}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$${GB}={a}−{R}=\frac{{a}−{b}}{\mathrm{2}} \\ $$$${GF}^{\mathrm{2}} ={GE}^{\mathrm{2}} −{EF}^{\mathrm{2}} =\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${GF}^{\mathrm{2}} ={GB}^{\mathrm{2}} +{BF}^{\mathrm{2}} =\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} =\mathrm{4}{ab} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{2}{ab} \\ $$
Commented by Tawa11 last updated on 29/Aug/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
