Question Number 152496 by mathdanisur last updated on 28/Aug/21
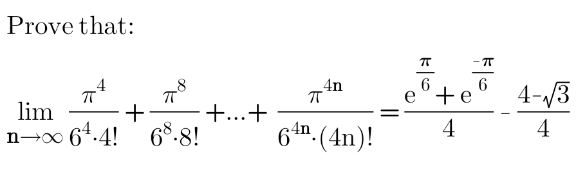
Answered by qaz last updated on 29/Aug/21
![Σ_(n=1) ^∞ (x^(4n) /((4n)!))=(x^4 /(4!))+(x^8 /(8!))+(x^(12) /(12!))+... =(1/2)[(1−(x^2 /(2!))+(x^4 /(4!))−...)+(1+(x^2 /(2!))+(x^4 /(4!))+...)]−1 =(1/2)cos x+(1/2)cosh x−1 ⇒Σ_(n=1) ^∞ (1/((4n)!))((π/6))^(4n) =(1/2)cos (π/6)+(1/2)cosh (π/6)−1=(1/4)(e^(π/6) +e^(−π/6) )−((4−(√3))/4)](https://www.tinkutara.com/question/Q152540.png)
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{x}^{\mathrm{4n}} }{\left(\mathrm{4n}\right)!}=\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{8}!}+\frac{\mathrm{x}^{\mathrm{12}} }{\mathrm{12}!}+… \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}−…\right)+\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}+…\right)\right]−\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosh}\:\mathrm{x}−\mathrm{1} \\ $$$$\Rightarrow\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4n}\right)!}\left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{4n}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cosh}\:\frac{\pi}{\mathrm{6}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{e}^{\pi/\mathrm{6}} +\mathrm{e}^{−\pi/\mathrm{6}} \right)−\frac{\mathrm{4}−\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
Commented by mathdanisur last updated on 29/Aug/21

$${thankyou}\:{Ser} \\ $$
