Menu Close

Question-152545

Tinku Tara 0 Comments
Pin




Question Number 152545 by liberty last updated on 29/Aug/21
Answered by Olaf_Thorendsen last updated on 31/Aug/21
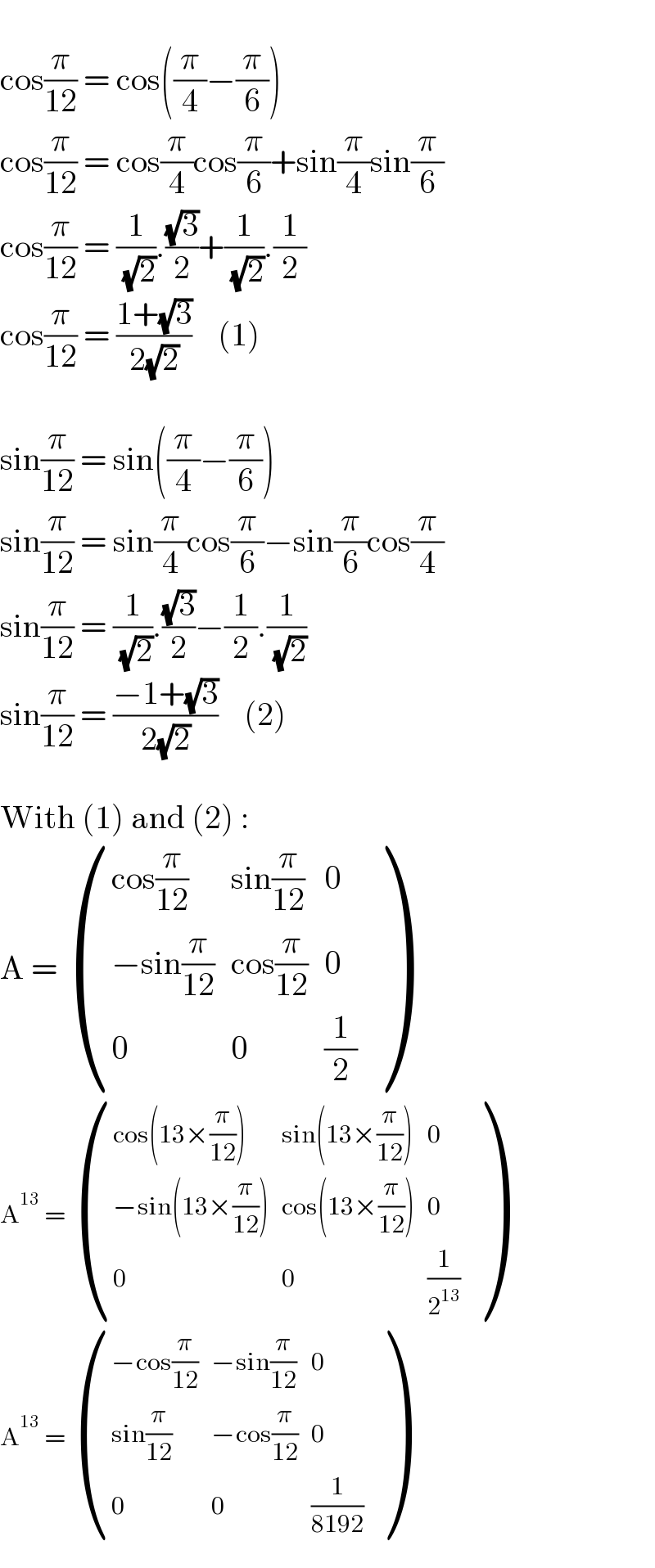
cos(π/(12)) = cos((π/4)−(π/6)) cos(π/(12)) = cos(π/4)cos(π/6)+sin(π/4)sin(π/6) cos(π/(12)) = (1/( (√2))).((√3)/2)+(1/( (√2))).(1/2) cos(π/(12)) = ((1+(√3))/(2(√2))) (1) sin(π/(12)) = sin((π/4)−(π/6)) sin(π/(12)) = sin(π/4)cos(π/6)−sin(π/6)cos(π/4) sin(π/(12)) = (1/( (√2))).((√3)/2)−(1/2).(1/( (√2))) sin(π/(12)) = ((−1+(√3))/(2(√2))) (2) With (1) and (2) : A = (((cos(π/(12))),(sin(π/(12))),0),((−sin(π/(12))),(cos(π/(12))),0),(0,0,(1/2)) ) A^(13) = (((cos(13×(π/(12)))),(sin(13×(π/(12)))),0),((−sin(13×(π/(12)))),(cos(13×(π/(12)))),0),(0,0,(1/2^(13) )) ) A^(13) = (((−cos(π/(12))),(−sin(π/(12))),0),((sin(π/(12))),(−cos(π/(12))),0),(0,0,(1/(8192))) )
$$\: \\ $$$$\mathrm{cos}\frac{\pi}{\mathrm{12}}\:=\:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{cos}\frac{\pi}{\mathrm{12}}\:=\:\mathrm{cos}\frac{\pi}{\mathrm{4}}\mathrm{cos}\frac{\pi}{\mathrm{6}}+\mathrm{sin}\frac{\pi}{\mathrm{4}}\mathrm{sin}\frac{\pi}{\mathrm{6}} \\ $$$$\mathrm{cos}\frac{\pi}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{cos}\frac{\pi}{\mathrm{12}}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{sin}\frac{\pi}{\mathrm{12}}\:=\:\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{sin}\frac{\pi}{\mathrm{12}}\:=\:\mathrm{sin}\frac{\pi}{\mathrm{4}}\mathrm{cos}\frac{\pi}{\mathrm{6}}−\mathrm{sin}\frac{\pi}{\mathrm{6}}\mathrm{cos}\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{sin}\frac{\pi}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{sin}\frac{\pi}{\mathrm{12}}\:=\:\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{With}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{A}\:=\:\begin{pmatrix}{\mathrm{cos}\frac{\pi}{\mathrm{12}}}&{\mathrm{sin}\frac{\pi}{\mathrm{12}}}&{\mathrm{0}}\\{−\mathrm{sin}\frac{\pi}{\mathrm{12}}}&{\mathrm{cos}\frac{\pi}{\mathrm{12}}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{2}}}\end{pmatrix} \\ $$$$\mathrm{A}^{\mathrm{13}} \:=\:\begin{pmatrix}{\mathrm{cos}\left(\mathrm{13}×\frac{\pi}{\mathrm{12}}\right)}&{\mathrm{sin}\left(\mathrm{13}×\frac{\pi}{\mathrm{12}}\right)}&{\mathrm{0}}\\{−\mathrm{sin}\left(\mathrm{13}×\frac{\pi}{\mathrm{12}}\right)}&{\mathrm{cos}\left(\mathrm{13}×\frac{\pi}{\mathrm{12}}\right)}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{13}} }}\end{pmatrix} \\ $$$$\mathrm{A}^{\mathrm{13}} \:=\:\begin{pmatrix}{−\mathrm{cos}\frac{\pi}{\mathrm{12}}}&{−\mathrm{sin}\frac{\pi}{\mathrm{12}}}&{\mathrm{0}}\\{\mathrm{sin}\frac{\pi}{\mathrm{12}}}&{−\mathrm{cos}\frac{\pi}{\mathrm{12}}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{8192}}}\end{pmatrix} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *