Question Number 152546 by liberty last updated on 29/Aug/21
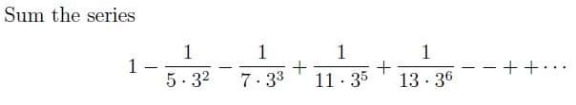
Answered by qaz last updated on 29/Aug/21
![1−(1/(5∙3^2 ))−(1/(7∙3^3 ))+(1/(11∙3^5 ))+(1/(13∙3^6 ))−(1/(17∙3^8 ))−(1/(19∙3^9 ))+... =(1−(1/(7∙3^3 ))+(1/(13∙3^6 ))−(1/(19∙3^9 ))+...+(((−1)^(n−1) )/([1+6(n−1)]∙3^(3(n−1)) ))+...)−((1/(5∙3^2 ))−(1/(11∙3^5 ))+(1/(17∙3^8 ))−...+(((−1)^(n−1) )/([5+6(n−1)]∙3^(2+3(n−1)) ))+...) =Σ_(n=0) ^∞ ((((−1)^n )/((1+6n)∙3^(3n) ))−(((−1)^n )/((5+6n)∙3^(2+3n) ))) =Σ_(n=0) ^∞ (((−1)^n )/(27^n ))((1/(1+6n))−(1/(45+54n))) =Σ_(n=0) ^∞ (((−1)^n )/(27^n ))∫_0 ^1 (x^(6n) −x^(54n+44) )dx =∫_0 ^1 (1/(1+(x^6 /(27))))−(x^(44) /(1+(x^(54) /(27))))dx =...](https://www.tinkutara.com/question/Q152560.png)
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}\centerdot\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{11}\centerdot\mathrm{3}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{13}\centerdot\mathrm{3}^{\mathrm{6}} }−\frac{\mathrm{1}}{\mathrm{17}\centerdot\mathrm{3}^{\mathrm{8}} }−\frac{\mathrm{1}}{\mathrm{19}\centerdot\mathrm{3}^{\mathrm{9}} }+… \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{3}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{13}\centerdot\mathrm{3}^{\mathrm{6}} }−\frac{\mathrm{1}}{\mathrm{19}\centerdot\mathrm{3}^{\mathrm{9}} }+…+\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\left[\mathrm{1}+\mathrm{6}\left(\mathrm{n}−\mathrm{1}\right)\right]\centerdot\mathrm{3}^{\mathrm{3}\left(\mathrm{n}−\mathrm{1}\right)} }+…\right)−\left(\frac{\mathrm{1}}{\mathrm{5}\centerdot\mathrm{3}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{11}\centerdot\mathrm{3}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{17}\centerdot\mathrm{3}^{\mathrm{8}} }−…+\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\left[\mathrm{5}+\mathrm{6}\left(\mathrm{n}−\mathrm{1}\right)\right]\centerdot\mathrm{3}^{\mathrm{2}+\mathrm{3}\left(\mathrm{n}−\mathrm{1}\right)} }+…\right) \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{1}+\mathrm{6n}\right)\centerdot\mathrm{3}^{\mathrm{3n}} }−\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{5}+\mathrm{6n}\right)\centerdot\mathrm{3}^{\mathrm{2}+\mathrm{3n}} }\right) \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{27}^{\mathrm{n}} }\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{6n}}−\frac{\mathrm{1}}{\mathrm{45}+\mathrm{54n}}\right) \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{27}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{6n}} −\mathrm{x}^{\mathrm{54n}+\mathrm{44}} \right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{27}}}−\frac{\mathrm{x}^{\mathrm{44}} }{\mathrm{1}+\frac{\mathrm{x}^{\mathrm{54}} }{\mathrm{27}}}\mathrm{dx} \\ $$$$=… \\ $$
