Question Number 152580 by aupo14 last updated on 29/Aug/21

Answered by Lordose last updated on 29/Aug/21
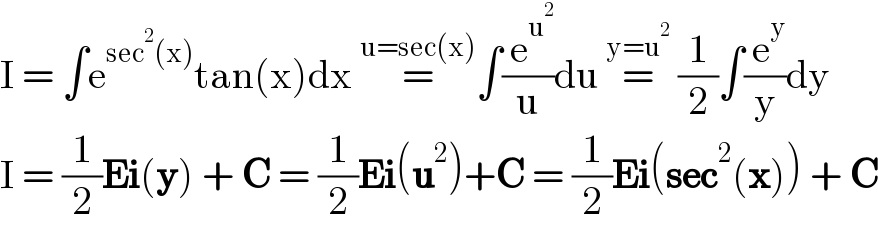
$$\mathrm{I}\:=\:\int\mathrm{e}^{\mathrm{sec}^{\mathrm{2}} \left(\mathrm{x}\right)} \mathrm{tan}\left(\mathrm{x}\right)\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{sec}\left(\mathrm{x}\right)} {=}\int\frac{\:\mathrm{e}^{\mathrm{u}^{\mathrm{2}} } }{\mathrm{u}}\mathrm{du}\:\overset{\mathrm{y}=\mathrm{u}^{\mathrm{2}} } {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\:\mathrm{e}^{\mathrm{y}} }{\mathrm{y}}\mathrm{dy} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{Ei}}\left(\boldsymbol{\mathrm{y}}\right)\:+\:\boldsymbol{\mathrm{C}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{Ei}}\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} \right)+\boldsymbol{\mathrm{C}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{Ei}}\left(\boldsymbol{\mathrm{sec}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)\right)\:+\:\boldsymbol{\mathrm{C}} \\ $$
