Question Number 152670 by liberty last updated on 31/Aug/21

Answered by Olaf_Thorendsen last updated on 31/Aug/21
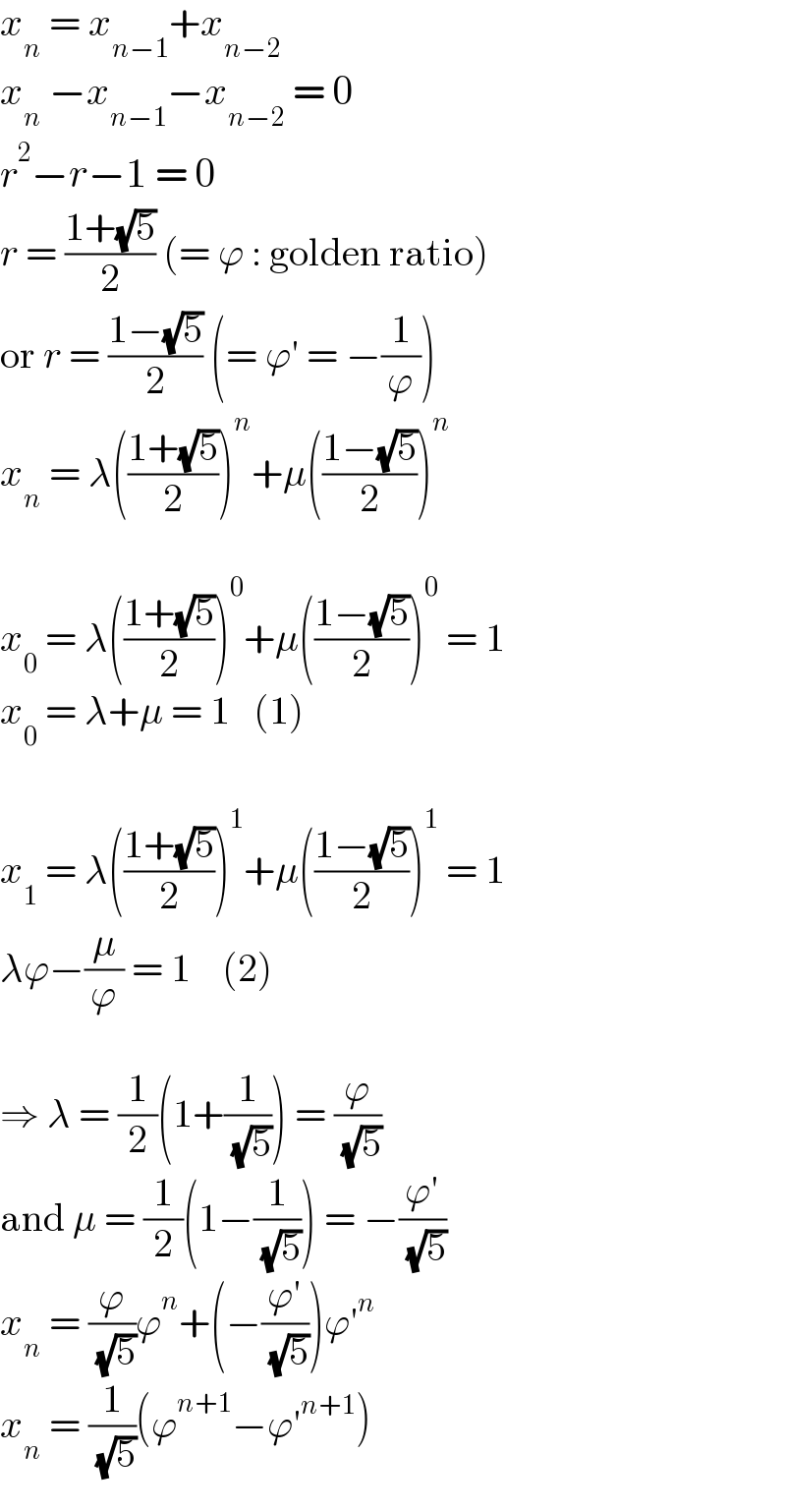
$${x}_{{n}} \:=\:{x}_{{n}−\mathrm{1}} +{x}_{{n}−\mathrm{2}} \\ $$$${x}_{{n}} \:−{x}_{{n}−\mathrm{1}} −{x}_{{n}−\mathrm{2}} \:=\:\mathrm{0} \\ $$$${r}^{\mathrm{2}} −{r}−\mathrm{1}\:=\:\mathrm{0} \\ $$$${r}\:=\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\left(=\:\varphi\::\:\mathrm{golden}\:\mathrm{ratio}\right) \\ $$$$\mathrm{or}\:{r}\:=\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\left(=\:\varphi'\:=\:−\frac{\mathrm{1}}{\varphi}\right) \\ $$$${x}_{{n}} \:=\:\lambda\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} +\mu\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \\ $$$$ \\ $$$${x}_{\mathrm{0}} \:=\:\lambda\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{0}} +\mu\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{0}} \:=\:\mathrm{1} \\ $$$${x}_{\mathrm{0}} \:=\:\lambda+\mu\:=\:\mathrm{1}\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${x}_{\mathrm{1}} \:=\:\lambda\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{1}} +\mu\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{1}} \:=\:\mathrm{1} \\ $$$$\lambda\varphi−\frac{\mu}{\varphi}\:=\:\mathrm{1}\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\Rightarrow\:\lambda\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\:=\:\frac{\varphi}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{and}\:\mu\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)\:=\:−\frac{\varphi'}{\:\sqrt{\mathrm{5}}} \\ $$$${x}_{{n}} \:=\:\frac{\varphi}{\:\sqrt{\mathrm{5}}}\varphi^{{n}} +\left(−\frac{\varphi'}{\:\sqrt{\mathrm{5}}}\right)\varphi'^{{n}} \\ $$$${x}_{{n}} \:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\varphi^{{n}+\mathrm{1}} −\varphi'^{{n}+\mathrm{1}} \right) \\ $$
Commented by puissant last updated on 31/Aug/21

$${Binet}\:{formula}.. \\ $$
