Question-152671

Question Number 152671 by liberty last updated on 31/Aug/21

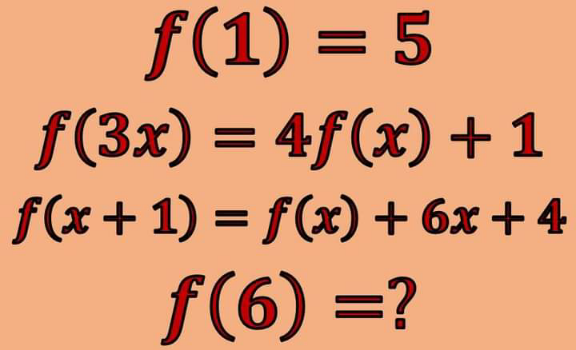
Commented by MJS_new last updated on 31/Aug/21

f(1)=5 f(2)=f(1+1)=f(1)+6×1+4=15 f(3)=f(2+1)=f(2)+6×2+4=31 but f(3)=f(3×1)=4f(1)+1=21 something′s wrong

$${f}\left(\mathrm{1}\right)=\mathrm{5} \\ $$$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right)+\mathrm{6}×\mathrm{1}+\mathrm{4}=\mathrm{15} \\ $$$${f}\left(\mathrm{3}\right)={f}\left(\mathrm{2}+\mathrm{1}\right)={f}\left(\mathrm{2}\right)+\mathrm{6}×\mathrm{2}+\mathrm{4}=\mathrm{31} \\ $$$$\mathrm{but} \\ $$$${f}\left(\mathrm{3}\right)={f}\left(\mathrm{3}×\mathrm{1}\right)=\mathrm{4}{f}\left(\mathrm{1}\right)+\mathrm{1}=\mathrm{21} \\ $$$$\mathrm{something}'\mathrm{s}\:\mathrm{wrong} \\ $$

Commented by liberty last updated on 31/Aug/21

from f(x+1)=f(x)+6x+4 x=1⇒f(2)=5+6+4=15 x=2⇒f(3)=15+12+4=31 x=3⇒f(4)=31+18+4=53 x=4⇒f(5)=53+24+4=91 x=5⇒f(6)=91+30+4=125 therefore fix the question something wrong

$$\mathrm{from}\:\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{6x}+\mathrm{4} \\ $$$$\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{f}\left(\mathrm{2}\right)=\mathrm{5}+\mathrm{6}+\mathrm{4}=\mathrm{15} \\ $$$$\mathrm{x}=\mathrm{2}\Rightarrow\mathrm{f}\left(\mathrm{3}\right)=\mathrm{15}+\mathrm{12}+\mathrm{4}=\mathrm{31} \\ $$$$\mathrm{x}=\mathrm{3}\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\mathrm{31}+\mathrm{18}+\mathrm{4}=\mathrm{53} \\ $$$$\mathrm{x}=\mathrm{4}\Rightarrow\mathrm{f}\left(\mathrm{5}\right)=\mathrm{53}+\mathrm{24}+\mathrm{4}=\mathrm{91} \\ $$$$\mathrm{x}=\mathrm{5}\Rightarrow\mathrm{f}\left(\mathrm{6}\right)=\mathrm{91}+\mathrm{30}+\mathrm{4}=\mathrm{125} \\ $$$$\mathrm{therefore}\:\mathrm{fix}\:\mathrm{the}\:\mathrm{question}\: \\ $$$$\mathrm{something}\:\mathrm{wrong} \\ $$

Answered by Rasheed.Sindhi last updated on 31/Aug/21

f(1)=5;f(3x)=4f(x)+1_((1)) ;f(x+1)=f(x)+6x+4_((2)) ;f(x)=? ^((2)⇒) f(1+1)=f(1)+6(1)+4=5+6+4=15 f(2)=15 ^((1)⇒) f(3×2)=4f(2)+1=4(15)+1=61 f(6)=61

$${f}\left(\mathrm{1}\right)=\mathrm{5};\underset{\left(\mathrm{1}\right)} {\underbrace{{f}\left(\mathrm{3}{x}\right)=\mathrm{4}{f}\left({x}\right)+\mathrm{1}}};\underset{\left(\mathrm{2}\right)} {\underbrace{{f}\left({x}+\mathrm{1}\right)={f}\left({x}\right)+\mathrm{6}{x}+\mathrm{4}}};{f}\left({x}\right)=? \\ $$$$\:^{\left(\mathrm{2}\right)\Rightarrow} {f}\left(\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right)+\mathrm{6}\left(\mathrm{1}\right)+\mathrm{4}=\mathrm{5}+\mathrm{6}+\mathrm{4}=\mathrm{15} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{15} \\ $$$$\:^{\left(\mathrm{1}\right)\Rightarrow} {f}\left(\mathrm{3}×\mathrm{2}\right)=\mathrm{4}{f}\left(\mathrm{2}\right)+\mathrm{1}=\mathrm{4}\left(\mathrm{15}\right)+\mathrm{1}=\mathrm{61} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{61} \\ $$

Answered by chengulapetrom last updated on 31/Aug/21

f(3(1))=4f(1)+1 f(3)=21 f(1+1)=f(1)+6+4 f(2)=15 f(3×2)=4f(2)+1 f(6)=4×15+1 f(6)=61

$${f}\left(\mathrm{3}\left(\mathrm{1}\right)\right)=\mathrm{4}{f}\left(\mathrm{1}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{21} \\ $$$${f}\left(\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right)+\mathrm{6}+\mathrm{4} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{15} \\ $$$${f}\left(\mathrm{3}×\mathrm{2}\right)=\mathrm{4}{f}\left(\mathrm{2}\right)+\mathrm{1} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{4}×\mathrm{15}+\mathrm{1} \\ $$$${f}\left(\mathrm{6}\right)=\mathrm{61} \\ $$

Answered by Olaf_Thorendsen last updated on 31/Aug/21

f(6) = f(3×2) = 4f(2)+1 = 4f(1+1)+1 = 4(f(1)+6×1+4)+1 = 4(5+10)+1 = 61

$${f}\left(\mathrm{6}\right)\:=\:{f}\left(\mathrm{3}×\mathrm{2}\right)\:=\:\mathrm{4}{f}\left(\mathrm{2}\right)+\mathrm{1} \\ $$$$=\:\mathrm{4}{f}\left(\mathrm{1}+\mathrm{1}\right)+\mathrm{1}\:=\:\mathrm{4}\left({f}\left(\mathrm{1}\right)+\mathrm{6}×\mathrm{1}+\mathrm{4}\right)+\mathrm{1} \\ $$$$=\:\mathrm{4}\left(\mathrm{5}+\mathrm{10}\right)+\mathrm{1}\:=\:\mathrm{61} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply