Question Number 152764 by mnjuly1970 last updated on 01/Sep/21
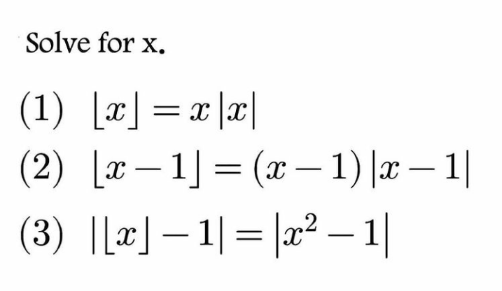
Commented by prakash jain last updated on 01/Sep/21

$$\left.\mathrm{1}\right)\:{x}={n}+{f} \\ $$$${n}\geqslant\mathrm{0} \\ $$$${n}=\left({n}+{f}\right)\left({n}+{f}\right)=\left({n}+{f}\right)^{\mathrm{2}} \\ $$$${f}^{\mathrm{2}} +\mathrm{2}{nf}+{n}\left({n}−\mathrm{1}\right)=\mathrm{0} \\ $$$${f}=\frac{−\mathrm{2}{n}\pm\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{4}{n}−\mathrm{4}{n}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${f}=−{n}\pm\sqrt{{n}} \\ $$$${n}=\mathrm{1},{f}=\mathrm{0} \\ $$$${n}=\mathrm{0},{f}=\mathrm{0} \\ $$$${n}<\mathrm{0} \\ $$$${n}=−\left({n}+{f}\right)^{\mathrm{2}} \\ $$$${f}^{\mathrm{2}} +\mathrm{2}{nf}+{n}\left({n}+\mathrm{1}\right)=\mathrm{0} \\ $$$${f}=−{n}\pm\sqrt{−{n}} \\ $$$${f}<\mathrm{1}\Rightarrow{no}\:{solution}\:{for}\:{n}<\mathrm{0}\:\left({wrong}\right) \\ $$$$\mathrm{A}\:\mathrm{mistake}\:\mathrm{pointed}\:\mathrm{by}\:\mathrm{mr}\:\mathrm{W}. \\ $$$$\mathrm{for}\:{n}<\mathrm{0}\: \\ $$$${n}=−\mathrm{1}\Rightarrow{f}=\mathrm{0} \\ $$$${x}=−\mathrm{1} \\ $$$${n}=−\mathrm{2}\Rightarrow{f}=\mathrm{2}−\sqrt{\mathrm{2}} \\ $$$${x}={n}+{f}=−\sqrt{\mathrm{2}} \\ $$$$−−−−−−−−−−− \\ $$$${x}=\mathrm{0}\:\mathrm{or}\:{x}=\mathrm{1} \\ $$$${x}=−\mathrm{1},\:{x}=−\sqrt{\mathrm{2}} \\ $$
Commented by mr W last updated on 01/Sep/21
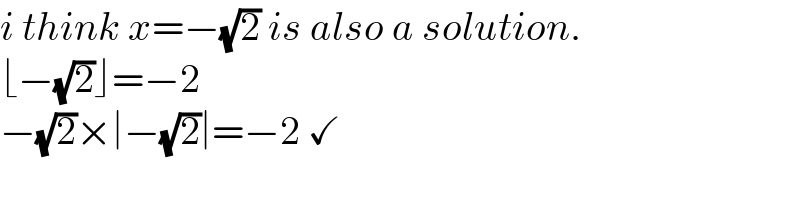
$${i}\:{think}\:{x}=−\sqrt{\mathrm{2}}\:{is}\:{also}\:{a}\:{solution}. \\ $$$$\lfloor−\sqrt{\mathrm{2}}\rfloor=−\mathrm{2} \\ $$$$−\sqrt{\mathrm{2}}×\mid−\sqrt{\mathrm{2}}\mid=−\mathrm{2}\:\checkmark \\ $$
Answered by prakash jain last updated on 01/Sep/21
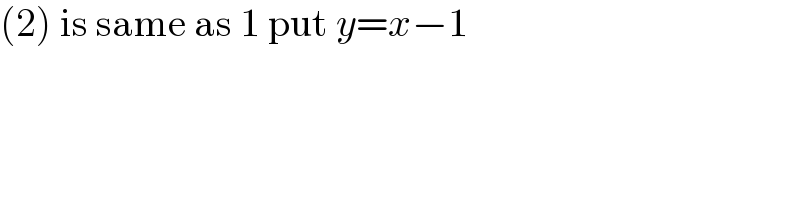
$$\left(\mathrm{2}\right)\:\mathrm{is}\:\mathrm{same}\:\mathrm{as}\:\mathrm{1}\:\mathrm{put}\:{y}={x}−\mathrm{1} \\ $$
Answered by MJS_new last updated on 02/Sep/21
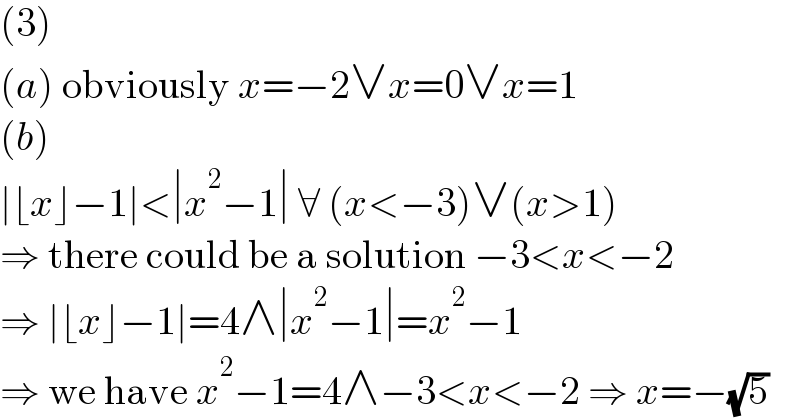
$$\left(\mathrm{3}\right) \\ $$$$\left({a}\right)\:\mathrm{obviously}\:{x}=−\mathrm{2}\vee{x}=\mathrm{0}\vee{x}=\mathrm{1} \\ $$$$\left({b}\right) \\ $$$$\mid\lfloor{x}\rfloor−\mathrm{1}\mid<\mid{x}^{\mathrm{2}} −\mathrm{1}\mid\:\forall\:\left({x}<−\mathrm{3}\right)\vee\left({x}>\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{there}\:\mathrm{could}\:\mathrm{be}\:\mathrm{a}\:\mathrm{solution}\:−\mathrm{3}<{x}<−\mathrm{2} \\ $$$$\Rightarrow\:\mid\lfloor{x}\rfloor−\mathrm{1}\mid=\mathrm{4}\wedge\mid{x}^{\mathrm{2}} −\mathrm{1}\mid={x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{have}\:{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{4}\wedge−\mathrm{3}<{x}<−\mathrm{2}\:\Rightarrow\:{x}=−\sqrt{\mathrm{5}} \\ $$
Answered by mnjuly1970 last updated on 02/Sep/21
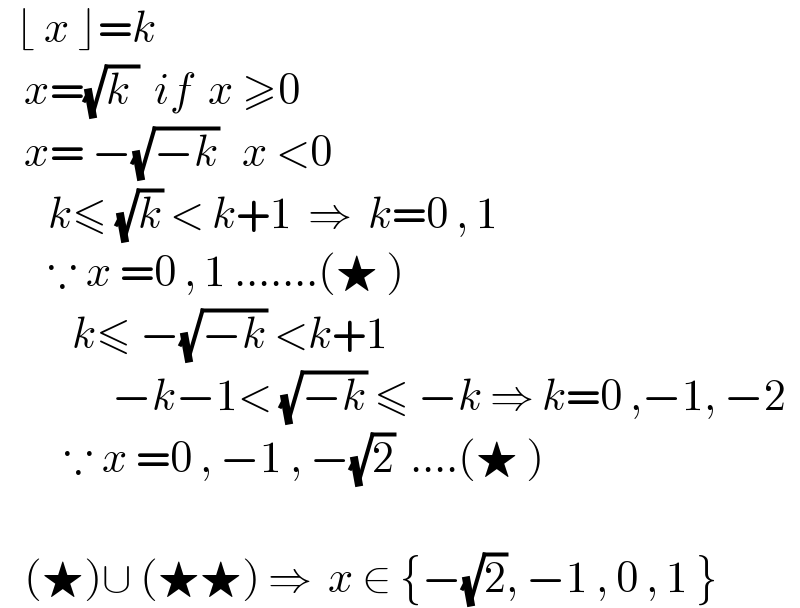
$$\:\:\lfloor\:{x}\:\rfloor={k}\: \\ $$$$\:\:\:{x}=\sqrt{{k}\:}\:\:{if}\:\:{x}\:\geqslant\mathrm{0} \\ $$$$\:\:\:{x}=\:−\sqrt{−{k}}\:\:\:{x}\:<\mathrm{0} \\ $$$$\:\:\:\:\:\:{k}\leqslant\:\sqrt{{k}}\:<\:{k}+\mathrm{1}\:\:\Rightarrow\:\:{k}=\mathrm{0}\:,\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\because\:{x}\:=\mathrm{0}\:,\:\mathrm{1}\:…….\left(\bigstar\:\right) \\ $$$$\:\:\:\:\:\:\:\:\:{k}\leqslant\:−\sqrt{−{k}}\:<{k}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{k}−\mathrm{1}<\:\sqrt{−{k}}\:\leqslant\:−{k}\:\Rightarrow\:{k}=\mathrm{0}\:,−\mathrm{1},\:−\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\because\:{x}\:=\mathrm{0}\:,\:−\mathrm{1}\:,\:−\sqrt{\mathrm{2}}\:\:….\left(\bigstar\:\right) \\ $$$$\:\:\: \\ $$$$\:\:\:\left(\bigstar\right)\cup\:\left(\bigstar\bigstar\right)\:\Rightarrow\:\:{x}\:\in\:\left\{−\sqrt{\mathrm{2}},\:−\mathrm{1}\:,\:\mathrm{0}\:,\:\mathrm{1}\:\right\}\: \\ $$
