Menu Close

Question-152769

Tinku Tara 0 Comments
Pin




Question Number 152769 by liberty last updated on 01/Sep/21
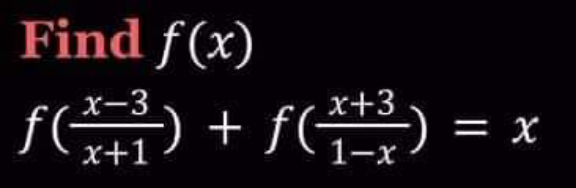
Commented by mathdanisur last updated on 01/Sep/21
f(x)=(x/2)+((x^2 +3)/(x^2 −1))
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$
Answered by tabata last updated on 01/Sep/21
let: y = ((x−3)/(x+1)) ⇒ xy + y = x−3 ⇒ x (y−1)=−3−y ⇒ x = ((3+y)/(1−y)) f(y) + f ( (((3+y+3−3y)/(1−y))/((1−y−3−y)/(1−y))) ) = ((3+y)/(1−y)) f(y) + f (((−3+y)/(1+y))) = ((3+y)/(1−y)) → (1) Replase y to x ⇒ f(x)+f (((−3+x)/(1+x)))=((3+x)/(1−x)) → (1) let: w = ((x+3)/(1−x)) ⇒ w − wx = x + 3 ⇒ w−3 = x(1+w)⇒ x = ((w−3)/(1+w)) f ( (((w−3−3−3w)/(1+w))/((w−3+1+w)/(1+w))) ) + f (w ) = ((w−3)/(1+w)) f ( ((3+w)/(1−w))) + f (w ) = ((w−3)/(1+w)) → (2) Replase w to x : f ( ((3+x)/(1−x))) + f (x) = ((x −3)/(1+x)) → (2) (1) + (2) ⇒ 2 f(x) + x = ((3+x)/(1−x)) + ((x −3)/(1+x)) 2 f (x) + x = (((3+x)(1+x)+(x−3)(1−x))/((1−x)(1+x))) 2 f (x) + x = ((8x)/(1−x^2 )) ⇒ f (x)= (1/2) ( ((8x−x+x^3 )/(1−x^2 )) ) ⟨ M . T ⟩
$$\boldsymbol{{let}}:\:\boldsymbol{{y}}\:=\:\frac{\boldsymbol{{x}}−\mathrm{3}}{\boldsymbol{{x}}+\mathrm{1}}\:\Rightarrow\:\boldsymbol{{xy}}\:+\:\boldsymbol{{y}}\:=\:\boldsymbol{{x}}−\mathrm{3}\:\Rightarrow\:\boldsymbol{{x}}\:\left(\boldsymbol{{y}}−\mathrm{1}\right)=−\mathrm{3}−\boldsymbol{{y}}\:\Rightarrow\:\boldsymbol{{x}}\:=\:\frac{\mathrm{3}+\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}} \\ $$$$ \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{y}}\right)\:+\:\boldsymbol{{f}}\:\left(\:\:\frac{\frac{\mathrm{3}+\boldsymbol{{y}}+\mathrm{3}−\mathrm{3}\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}}}{\frac{\mathrm{1}−\boldsymbol{{y}}−\mathrm{3}−\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}}}\:\:\right)\:=\:\frac{\mathrm{3}+\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}}\: \\ $$$$ \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{y}}\right)\:+\:\boldsymbol{{f}}\:\left(\frac{−\mathrm{3}+\boldsymbol{{y}}}{\mathrm{1}+\boldsymbol{{y}}}\right)\:=\:\frac{\mathrm{3}+\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}}\:\rightarrow\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\boldsymbol{{Replase}}\:\boldsymbol{{y}}\:\boldsymbol{{to}}\:\boldsymbol{{x}}\:\Rightarrow\: \\ $$$$ \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)+\boldsymbol{{f}}\:\left(\frac{−\mathrm{3}+\boldsymbol{{x}}}{\mathrm{1}+\boldsymbol{{x}}}\right)=\frac{\mathrm{3}+\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}}\:\rightarrow\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\boldsymbol{{let}}:\:\boldsymbol{{w}}\:=\:\frac{\boldsymbol{{x}}+\mathrm{3}}{\mathrm{1}−\boldsymbol{{x}}}\:\Rightarrow\:\boldsymbol{{w}}\:−\:\boldsymbol{{wx}}\:=\:\boldsymbol{{x}}\:+\:\mathrm{3}\:\Rightarrow\:\boldsymbol{{w}}−\mathrm{3}\:=\:\boldsymbol{{x}}\left(\mathrm{1}+\boldsymbol{{w}}\right)\Rightarrow\:\boldsymbol{{x}}\:=\:\frac{\boldsymbol{{w}}−\mathrm{3}}{\mathrm{1}+\boldsymbol{{w}}} \\ $$$$ \\ $$$$\boldsymbol{{f}}\:\left(\:\frac{\frac{\boldsymbol{{w}}−\mathrm{3}−\mathrm{3}−\mathrm{3}\boldsymbol{{w}}}{\mathrm{1}+\boldsymbol{{w}}}}{\frac{\boldsymbol{{w}}−\mathrm{3}+\mathrm{1}+\boldsymbol{{w}}}{\mathrm{1}+\boldsymbol{{w}}}}\:\right)\:+\:\boldsymbol{{f}}\:\left(\boldsymbol{{w}}\:\right)\:=\:\frac{\boldsymbol{{w}}−\mathrm{3}}{\mathrm{1}+\boldsymbol{{w}}} \\ $$$$ \\ $$$$\boldsymbol{{f}}\:\left(\:\frac{\mathrm{3}+\boldsymbol{{w}}}{\mathrm{1}−\boldsymbol{{w}}}\right)\:+\:\boldsymbol{{f}}\:\left(\boldsymbol{{w}}\:\right)\:=\:\frac{\boldsymbol{{w}}−\mathrm{3}}{\mathrm{1}+\boldsymbol{{w}}}\:\rightarrow\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\boldsymbol{{Replase}}\:\boldsymbol{{w}}\:\boldsymbol{{to}}\:\boldsymbol{{x}}\:: \\ $$$$ \\ $$$$\boldsymbol{{f}}\:\left(\:\frac{\mathrm{3}+\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}}\right)\:+\:\boldsymbol{{f}}\:\left(\boldsymbol{{x}}\right)\:=\:\frac{\boldsymbol{{x}}\:−\mathrm{3}}{\mathrm{1}+\boldsymbol{{x}}}\:\rightarrow\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:+\:\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{2}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{x}}\:=\:\frac{\mathrm{3}+\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}}\:+\:\frac{\boldsymbol{{x}}\:−\mathrm{3}}{\mathrm{1}+\boldsymbol{{x}}} \\ $$$$ \\ $$$$\mathrm{2}\:\boldsymbol{{f}}\:\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{x}}\:=\:\frac{\left(\mathrm{3}+\boldsymbol{{x}}\right)\left(\mathrm{1}+\boldsymbol{{x}}\right)+\left(\boldsymbol{{x}}−\mathrm{3}\right)\left(\mathrm{1}−\boldsymbol{{x}}\right)}{\left(\mathrm{1}−\boldsymbol{{x}}\right)\left(\mathrm{1}+\boldsymbol{{x}}\right)} \\ $$$$ \\ $$$$\mathrm{2}\:\boldsymbol{{f}}\:\left(\boldsymbol{{x}}\right)\:+\:\boldsymbol{{x}}\:=\:\frac{\mathrm{8}\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:\Rightarrow\:\boldsymbol{{f}}\:\left(\boldsymbol{{x}}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\:\frac{\mathrm{8}\boldsymbol{{x}}−\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:\right) \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *