Question Number 152829 by liberty last updated on 01/Sep/21
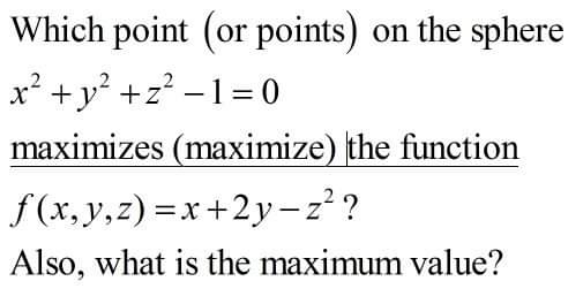
Answered by MJS_new last updated on 02/Sep/21

$${z}^{\mathrm{2}} =\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$$\Rightarrow\:{f}\left({x},\:{y},\:{z}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{x}+\mathrm{2}{y}−\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{obviously}\:{x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0}\:\mathrm{to}\:\mathrm{get}\:\mathrm{a}\:\mathrm{maximum} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{obviously}\:{x}\leqslant\mathrm{1}\wedge{y}\leqslant\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1}\:\Rightarrow\:\mathrm{max}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:=\mathrm{1}\:\mathrm{with}\:{y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{f}\left({x},\:{y},\:{z}\right)={x}+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{f}\:'=\mathrm{1}−\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\:\Rightarrow\:{y}=\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{5}}\:\Rightarrow\:{z}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{max}\:\left({f}\left({x},\:{y},\:{z}\right)\right)\:=\sqrt{\mathrm{5}} \\ $$
Answered by mr W last updated on 02/Sep/21

$${such}\:{that}\:{f}\left({x},{y},{z}\right)={x}+\mathrm{2}{y}−{z}^{\mathrm{2}} \:{is}\:{max}. \\ $$$$\Rightarrow{z}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\:\Rightarrow{x}=\mathrm{cos}\:\theta,\:{y}=\mathrm{sin}\:\theta \\ $$$${f}=\mathrm{cos}\:\theta+\mathrm{2sin}\:\theta=\sqrt{\mathrm{5}}\:\mathrm{cos}\:\left(\theta−\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\right) \\ $$$${f}_{{max}} =\sqrt{\mathrm{5}} \\ $$$${at}\:\theta=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\:\Rightarrow{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}},\:{y}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}},\:{z}=\mathrm{0} \\ $$
