Question Number 152841 by 0731619 last updated on 02/Sep/21

Answered by bobhans last updated on 02/Sep/21
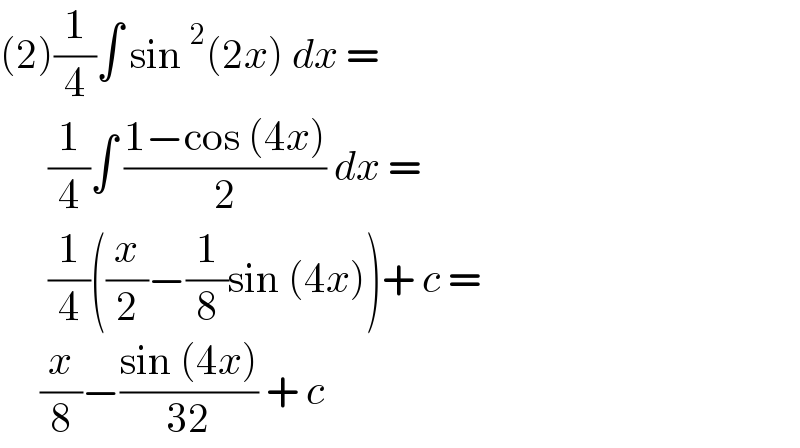
$$\left(\mathrm{2}\right)\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:{dx}\:= \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{4}{x}\right)}{\mathrm{2}}\:{dx}\:= \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{x}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\left(\mathrm{4}{x}\right)\right)+\:{c}\:= \\ $$$$\:\:\:\:\:\frac{{x}}{\mathrm{8}}−\frac{\mathrm{sin}\:\left(\mathrm{4}{x}\right)}{\mathrm{32}}\:+\:{c} \\ $$
Answered by bobhans last updated on 02/Sep/21
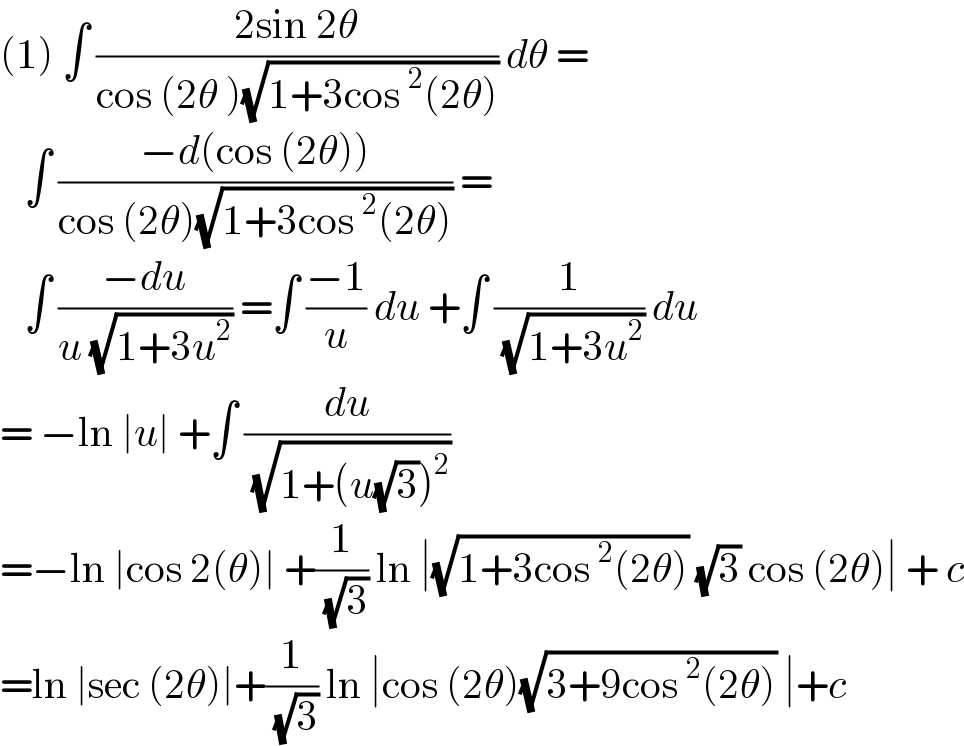
$$\left(\mathrm{1}\right)\:\int\:\frac{\mathrm{2sin}\:\mathrm{2}\theta}{\mathrm{cos}\:\left(\mathrm{2}\theta\:\right)\sqrt{\mathrm{1}+\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{2}\theta\right)}}\:{d}\theta\:= \\ $$$$\:\:\:\int\:\frac{−{d}\left(\mathrm{cos}\:\left(\mathrm{2}\theta\right)\right)}{\mathrm{cos}\:\left(\mathrm{2}\theta\right)\sqrt{\mathrm{1}+\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{2}\theta\right)}}\:= \\ $$$$\:\:\:\int\:\frac{−{du}}{{u}\:\sqrt{\mathrm{1}+\mathrm{3}{u}^{\mathrm{2}} }}\:=\int\:\frac{−\mathrm{1}}{{u}}\:{du}\:+\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{3}{u}^{\mathrm{2}} }}\:{du} \\ $$$$=\:−\mathrm{ln}\:\mid{u}\mid\:+\int\:\frac{{du}}{\:\sqrt{\mathrm{1}+\left({u}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }}\: \\ $$$$=−\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{2}\left(\theta\right)\mid\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\mid\sqrt{\mathrm{1}+\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{2}\theta\right)}\:\sqrt{\mathrm{3}}\:\mathrm{cos}\:\left(\mathrm{2}\theta\right)\mid\:+\:{c} \\ $$$$=\mathrm{ln}\:\mid\mathrm{sec}\:\left(\mathrm{2}\theta\right)\mid+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\mid\mathrm{cos}\:\left(\mathrm{2}\theta\right)\sqrt{\mathrm{3}+\mathrm{9cos}\:^{\mathrm{2}} \left(\mathrm{2}\theta\right)}\:\mid+{c} \\ $$
Commented by peter frank last updated on 03/Sep/21

$$\mathrm{good} \\ $$
