Question-152904

Question Number 152904 by DELETED last updated on 03/Sep/21

Answered by DELETED last updated on 03/Sep/21

1). f(x)=4cos x+5sin x (dy/dx) =−4 sin x+5 cos × 2). f(x)=3 sin 2x − 5 cos x (dy/dx) =3×2 cos 2x +5 sin x =6 cos 2x + 5 sin x// 3). f(x)= tan (2x+1) (dy/dx) = 2 sec^2 (2x+1)// 4). f(x)= ((sin x + cos x)/(sin x)) = 1 + cot x (dy/dx) = −cosec^2 x

$$\left.\mathrm{1}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{4cos}\:\mathrm{x}+\mathrm{5sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:\:=−\mathrm{4}\:\mathrm{sin}\:\mathrm{x}+\mathrm{5}\:\mathrm{cos}\:× \\ $$$$\left.\mathrm{2}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}\:\mathrm{sin}\:\mathrm{2x}\:−\:\mathrm{5}\:\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:=\mathrm{3}×\mathrm{2}\:\mathrm{cos}\:\mathrm{2x}\:+\mathrm{5}\:\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}\:\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{5}\:\mathrm{sin}\:\mathrm{x}// \\ $$$$\left.\mathrm{3}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{tan}\:\left(\mathrm{2x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{2}\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right)// \\ $$$$\left.\mathrm{4}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\:+\:\mathrm{cot}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:−\mathrm{cosec}\:^{\mathrm{2}} \:\mathrm{x} \\ $$

Answered by DELETED last updated on 03/Sep/21

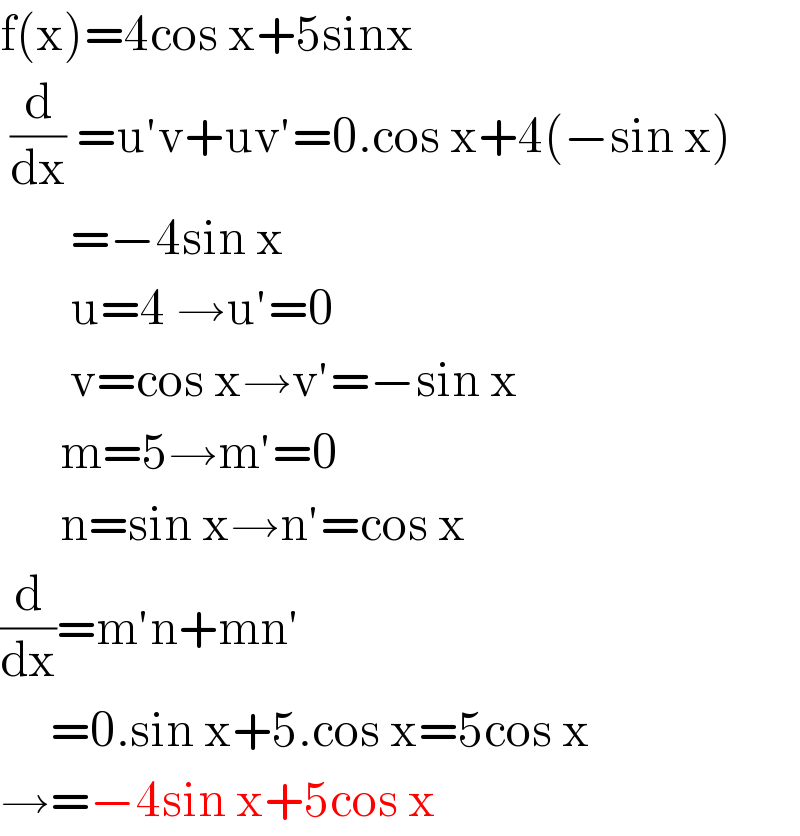
f(x)=4cos x+5sinx (d/dx) =u′v+uv′=0.cos x+4(−sin x) =−4sin x u=4 →u′=0 v=cos x→v′=−sin x m=5→m′=0 n=sin x→n′=cos x (d/dx)=m′n+mn′ =0.sin x+5.cos x=5cos x →=−4sin x+5cos x

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{4cos}\:\mathrm{x}+\mathrm{5sinx} \\ $$$$\:\frac{\mathrm{d}}{\mathrm{dx}}\:=\mathrm{u}'\mathrm{v}+\mathrm{uv}'=\mathrm{0}.\mathrm{cos}\:\mathrm{x}+\mathrm{4}\left(−\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:=−\mathrm{4sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\mathrm{u}=\mathrm{4}\:\rightarrow\mathrm{u}'=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{v}=\mathrm{cos}\:\mathrm{x}\rightarrow\mathrm{v}'=−\mathrm{sin}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\mathrm{m}=\mathrm{5}\rightarrow\mathrm{m}'=\mathrm{0} \\ $$$$\:\:\:\:\:\:\mathrm{n}=\mathrm{sin}\:\mathrm{x}\rightarrow\mathrm{n}'=\mathrm{cos}\:\mathrm{x} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}=\mathrm{m}'\mathrm{n}+\mathrm{mn}' \\ $$$$\:\:\:\:\:=\mathrm{0}.\mathrm{sin}\:\mathrm{x}+\mathrm{5}.\mathrm{cos}\:\mathrm{x}=\mathrm{5cos}\:\mathrm{x} \\ $$$$\rightarrow=−\mathrm{4sin}\:\mathrm{x}+\mathrm{5cos}\:\mathrm{x} \\ $$

Answered by DELETED last updated on 03/Sep/21

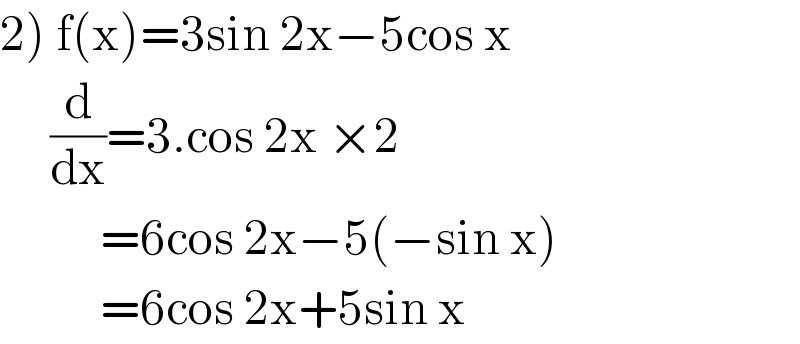
2) f(x)=3sin 2x−5cos x (d/dx)=3.cos 2x ×2 =6cos 2x−5(−sin x) =6cos 2x+5sin x

$$\left.\mathrm{2}\right)\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3sin}\:\mathrm{2x}−\mathrm{5cos}\:\mathrm{x} \\ $$$$\:\:\:\:\:\frac{\mathrm{d}}{\mathrm{dx}}=\mathrm{3}.\mathrm{cos}\:\mathrm{2x}\:×\mathrm{2}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{6cos}\:\mathrm{2x}−\mathrm{5}\left(−\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{6cos}\:\mathrm{2x}+\mathrm{5sin}\:\mathrm{x} \\ $$

Answered by DELETED last updated on 03/Sep/21

3). f′(x)=sec^2 (2x+1)(2) =2 sec^2 (2x+1)

$$\left.\mathrm{3}\right).\:\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right)\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\:\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right) \\ $$

Answered by DELETED last updated on 03/Sep/21

4). f(x)=((sin x+cos x)/(sin x))=1+cot x (d/dx)=0−cosec^2 x=−cosec^2 x

$$\left.\mathrm{4}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}=\mathrm{1}+\mathrm{cot}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{d}}{\mathrm{dx}}=\mathrm{0}−\mathrm{cosec}^{\mathrm{2}} \mathrm{x}=−\mathrm{cosec}\:^{\mathrm{2}} \:\mathrm{x} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply