Question Number 152912 by mathdanisur last updated on 03/Sep/21

Answered by ghimisi last updated on 03/Sep/21
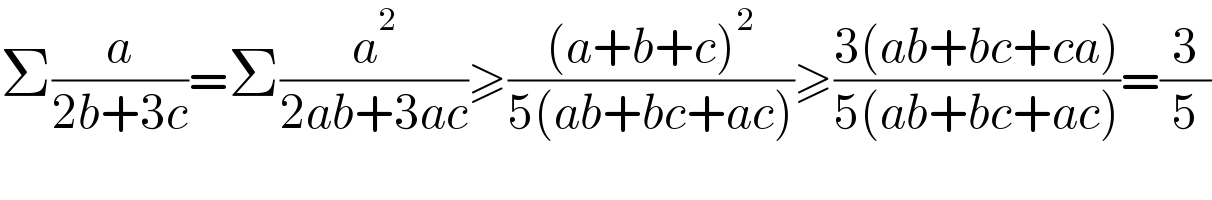
$$\Sigma\frac{{a}}{\mathrm{2}{b}+\mathrm{3}{c}}=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{2}{ab}+\mathrm{3}{ac}}\geqslant\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} }{\mathrm{5}\left({ab}+{bc}+{ac}\right)}\geqslant\frac{\mathrm{3}\left({ab}+{bc}+{ca}\right)}{\mathrm{5}\left({ab}+{bc}+{ac}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Commented by ghimisi last updated on 03/Sep/21
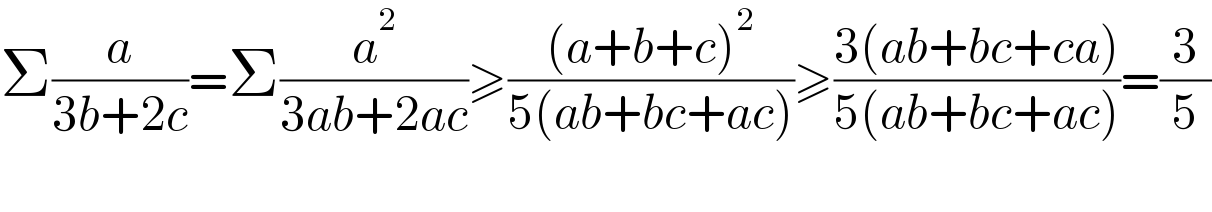
$$\Sigma\frac{{a}}{\mathrm{3}{b}+\mathrm{2}{c}}=\Sigma\frac{{a}^{\mathrm{2}} }{\mathrm{3}{ab}+\mathrm{2}{ac}}\geqslant\frac{\left({a}+{b}+{c}\right)^{\mathrm{2}} }{\mathrm{5}\left({ab}+{bc}+{ac}\right)}\geqslant\frac{\mathrm{3}\left({ab}+{bc}+{ca}\right)}{\mathrm{5}\left({ab}+{bc}+{ac}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 03/Sep/21

$$\mathrm{Nice}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{thank}\:\mathrm{you} \\ $$
