Question Number 152935 by DELETED last updated on 03/Sep/21

Answered by DELETED last updated on 03/Sep/21
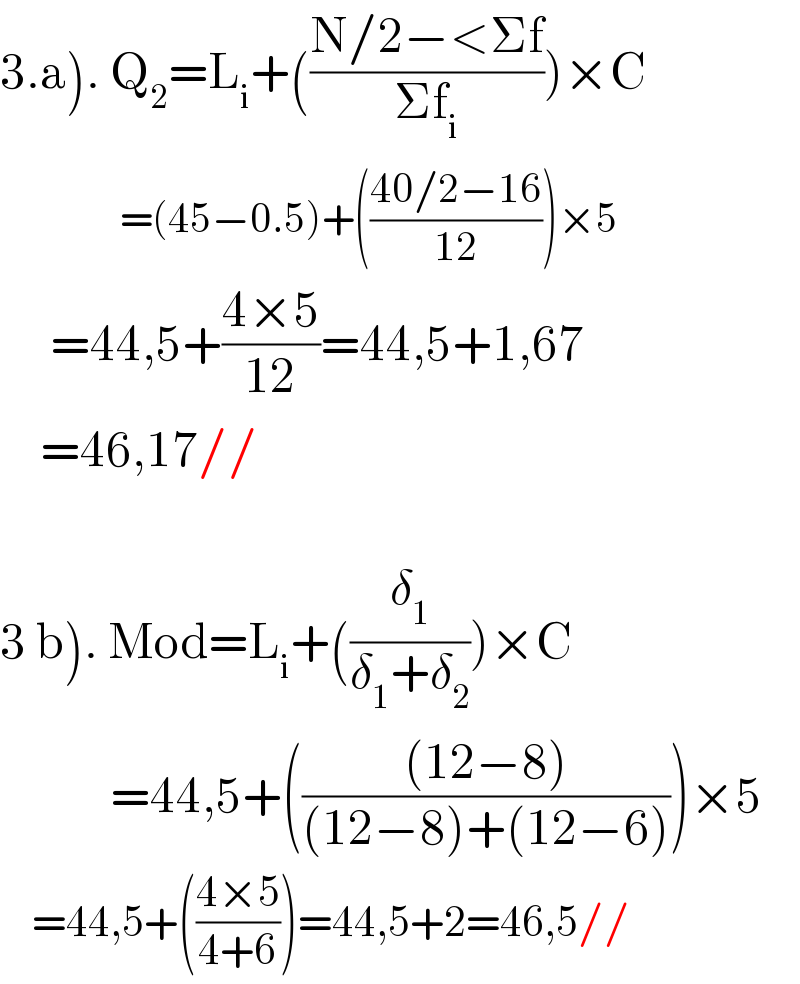
$$\left.\mathrm{3}.\mathrm{a}\right).\:\mathrm{Q}_{\mathrm{2}} =\mathrm{L}_{\mathrm{i}} +\left(\frac{\mathrm{N}/\mathrm{2}−<\Sigma\mathrm{f}}{\Sigma\mathrm{f}_{\mathrm{i}} }\right)×\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{45}−\mathrm{0}.\mathrm{5}\right)+\left(\frac{\mathrm{40}/\mathrm{2}−\mathrm{16}}{\mathrm{12}}\right)×\mathrm{5} \\ $$$$\:\:\:\:\:=\mathrm{44},\mathrm{5}+\frac{\mathrm{4}×\mathrm{5}}{\mathrm{12}}=\mathrm{44},\mathrm{5}+\mathrm{1},\mathrm{67} \\ $$$$\:\:\:\:=\mathrm{46},\mathrm{17}// \\ $$$$ \\ $$$$\left.\mathrm{3}\:\mathrm{b}\right).\:\mathrm{Mod}=\mathrm{L}_{\mathrm{i}} +\left(\frac{\delta_{\mathrm{1}} }{\delta_{\mathrm{1}} +\delta_{\mathrm{2}} }\right)×\mathrm{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{44},\mathrm{5}+\left(\frac{\left(\mathrm{12}−\mathrm{8}\right)}{\left(\mathrm{12}−\mathrm{8}\right)+\left(\mathrm{12}−\mathrm{6}\right)}\right)×\mathrm{5} \\ $$$$\:\:\:\:=\mathrm{44},\mathrm{5}+\left(\frac{\mathrm{4}×\mathrm{5}}{\mathrm{4}+\mathrm{6}}\right)=\mathrm{44},\mathrm{5}+\mathrm{2}=\mathrm{46},\mathrm{5}// \\ $$
