Question Number 152985 by ajfour last updated on 03/Sep/21
Commented by mr W last updated on 03/Sep/21

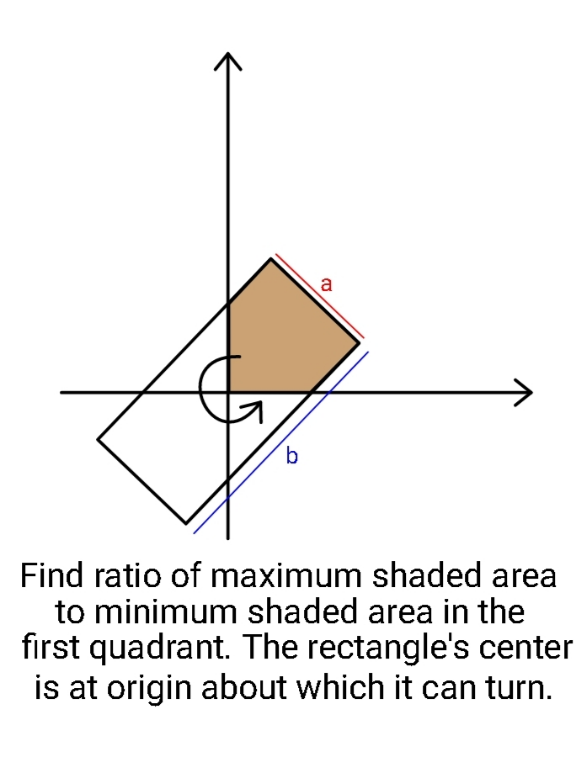
$${area}\:{in}\:{first}\:{quadrant}\: \\ $$$$+\:{area}\:{in}\:{second}\:{quadrant}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{of}\:{rectangle}\:=\:{constant} \\ $$$${i}.{e}.\:{when}\:{area}\:{in}\:{first}\:{quadrant}\:{is} \\ $$$${maximum},\:{the}\:{area}\:{in}\:{second}\: \\ $$$${quadrant}\:{is}\:{minimum},\:{and}\:{vice}\:{versa}. \\ $$$${A}_{{min}} =\frac{\mathrm{1}}{\mathrm{2}}×{a}×\frac{{a}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}_{{max}} =\frac{{ab}}{\mathrm{2}}−\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\frac{{A}_{{max}} }{{A}_{{min}} }=\frac{\mathrm{2}{b}}{{a}}−\mathrm{1} \\ $$$$\left({assume}\:{a}\leqslant{b}\right) \\ $$
Commented by ajfour last updated on 03/Sep/21
$${thanks}\:{sir};\:{love}\:{the}\:{way}\:{you} \\ $$$${present}\:{it}! \\ $$
