Question Number 153054 by daus last updated on 04/Sep/21

Answered by bobhans last updated on 04/Sep/21
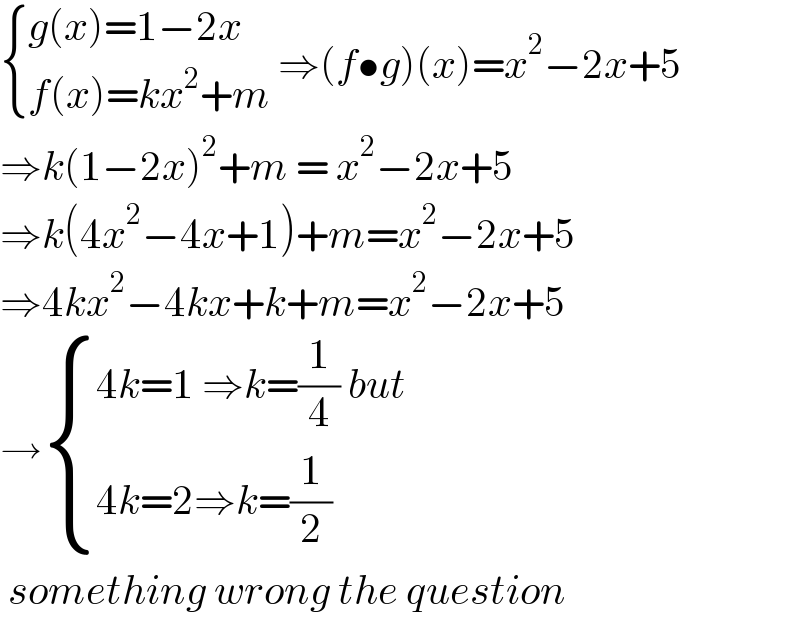
$$\begin{cases}{{g}\left({x}\right)=\mathrm{1}−\mathrm{2}{x}}\\{{f}\left({x}\right)={kx}^{\mathrm{2}} +{m}}\end{cases}\:\Rightarrow\left({f}\bullet{g}\right)\left({x}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\Rightarrow{k}\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{2}} +{m}\:=\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\Rightarrow{k}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}\right)+{m}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\Rightarrow\mathrm{4}{kx}^{\mathrm{2}} −\mathrm{4}{kx}+{k}+{m}={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5} \\ $$$$\rightarrow\begin{cases}{\mathrm{4}{k}=\mathrm{1}\:\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{4}}\:{but}}\\{\mathrm{4}{k}=\mathrm{2}\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$$\:{something}\:{wrong}\:{the}\:{question} \\ $$
