Question Number 153057 by DELETED last updated on 04/Sep/21
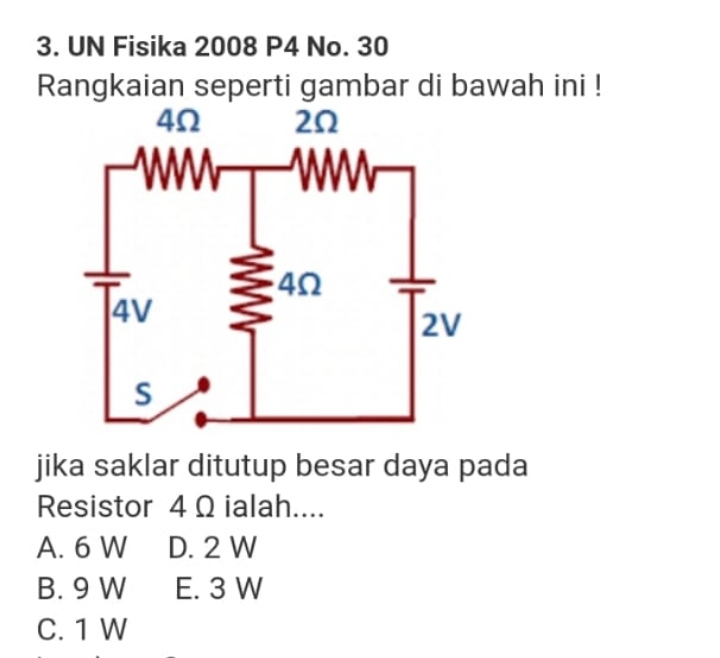
Answered by DELETED last updated on 04/Sep/21
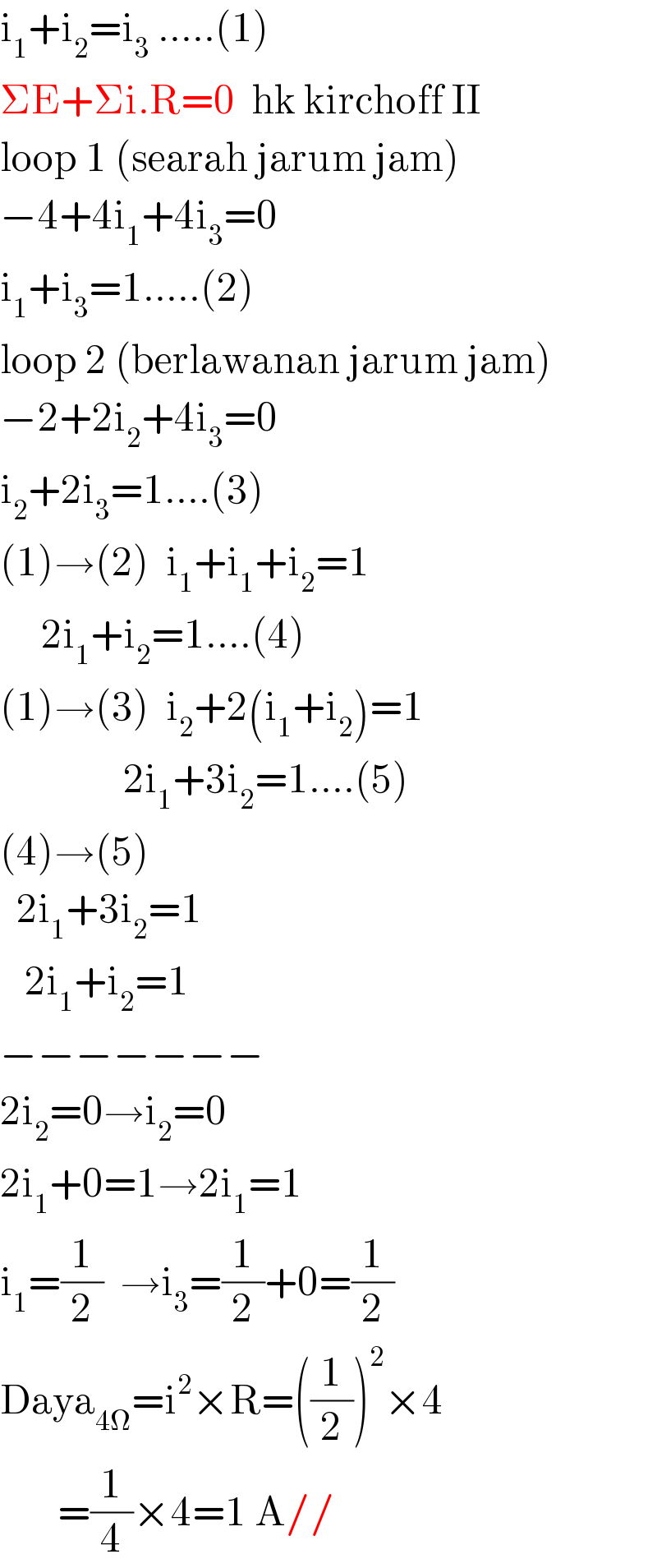
$$\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{i}_{\mathrm{3}} \:…..\left(\mathrm{1}\right) \\ $$$$\Sigma\mathrm{E}+\Sigma\mathrm{i}.\mathrm{R}=\mathrm{0}\:\:\mathrm{hk}\:\mathrm{kirchoff}\:\mathrm{II} \\ $$$$\mathrm{loop}\:\mathrm{1}\:\left(\mathrm{searah}\:\mathrm{jarum}\:\mathrm{jam}\right) \\ $$$$−\mathrm{4}+\mathrm{4i}_{\mathrm{1}} +\mathrm{4i}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{3}} =\mathrm{1}…..\left(\mathrm{2}\right)\: \\ $$$$\mathrm{loop}\:\mathrm{2}\:\left(\mathrm{berlawanan}\:\mathrm{jarum}\:\mathrm{jam}\right) \\ $$$$−\mathrm{2}+\mathrm{2i}_{\mathrm{2}} +\mathrm{4i}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{i}_{\mathrm{2}} +\mathrm{2i}_{\mathrm{3}} =\mathrm{1}….\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)\rightarrow\left(\mathrm{2}\right)\:\:\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{1}….\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{1}\right)\rightarrow\left(\mathrm{3}\right)\:\:\mathrm{i}_{\mathrm{2}} +\mathrm{2}\left(\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} \right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{1}….\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right)\rightarrow\left(\mathrm{5}\right) \\ $$$$\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{1} \\ $$$$−−−−−−− \\ $$$$\mathrm{2i}_{\mathrm{2}} =\mathrm{0}\rightarrow\mathrm{i}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{2i}_{\mathrm{1}} +\mathrm{0}=\mathrm{1}\rightarrow\mathrm{2i}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{i}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:\rightarrow\mathrm{i}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{0}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{Daya}_{\mathrm{4}\Omega} =\mathrm{i}^{\mathrm{2}} ×\mathrm{R}=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} ×\mathrm{4} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{4}=\mathrm{1}\:\mathrm{A}// \\ $$
