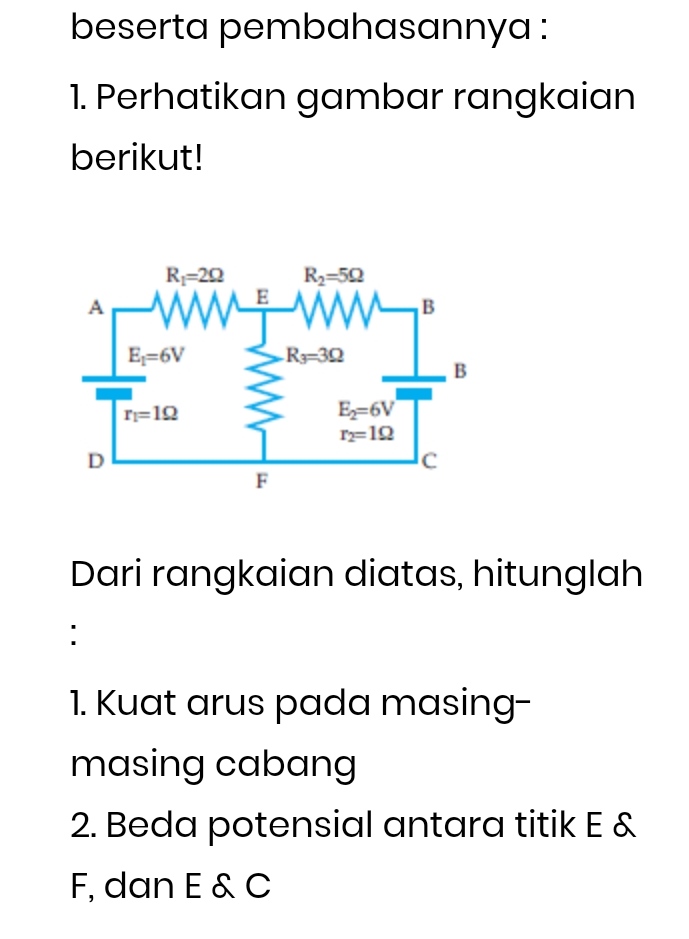
Question Number 153173 by DELETED last updated on 05/Sep/21
Commented by mr W last updated on 05/Sep/21

$${dear}\:{sir}: \\ $$$${if}\:{you}\:{just}\:{do}\:{your}\:{own}\:{exercises},\:{i}.{e}. \\ $$$${when}\:{you}\:{solve}\:{your}\:{questions}\:{by} \\ $$$${yourself},\:{you}\:{don}'{t}\:{need}\:{to}\:{use}\:{the} \\ $$$${forum}\:{function}\:{of}\:{this}\:{app}.\:{forum} \\ $$$${function}\:{is}\:{for}\:{exchanging}\:{with} \\ $$$${other}\:{people},\:{i}.{e}.\:{other}\:{people}\:{help} \\ $$$${you}\:{to}\:{solve}\:{your}\:{questions}\:{or}\:{you} \\ $$$${help}\:{other}\:{people}\:{to}\:{solve}\:{their} \\ $$$${questions}.\:\:{in}\:{forum}\:{please}\:{use}\:{a} \\ $$$${language}\:{which}\:{other}\:{people}\:{may} \\ $$$${understand},\:{generally}\:{english}.\:{thanks}! \\ $$
Answered by DELETED last updated on 05/Sep/21
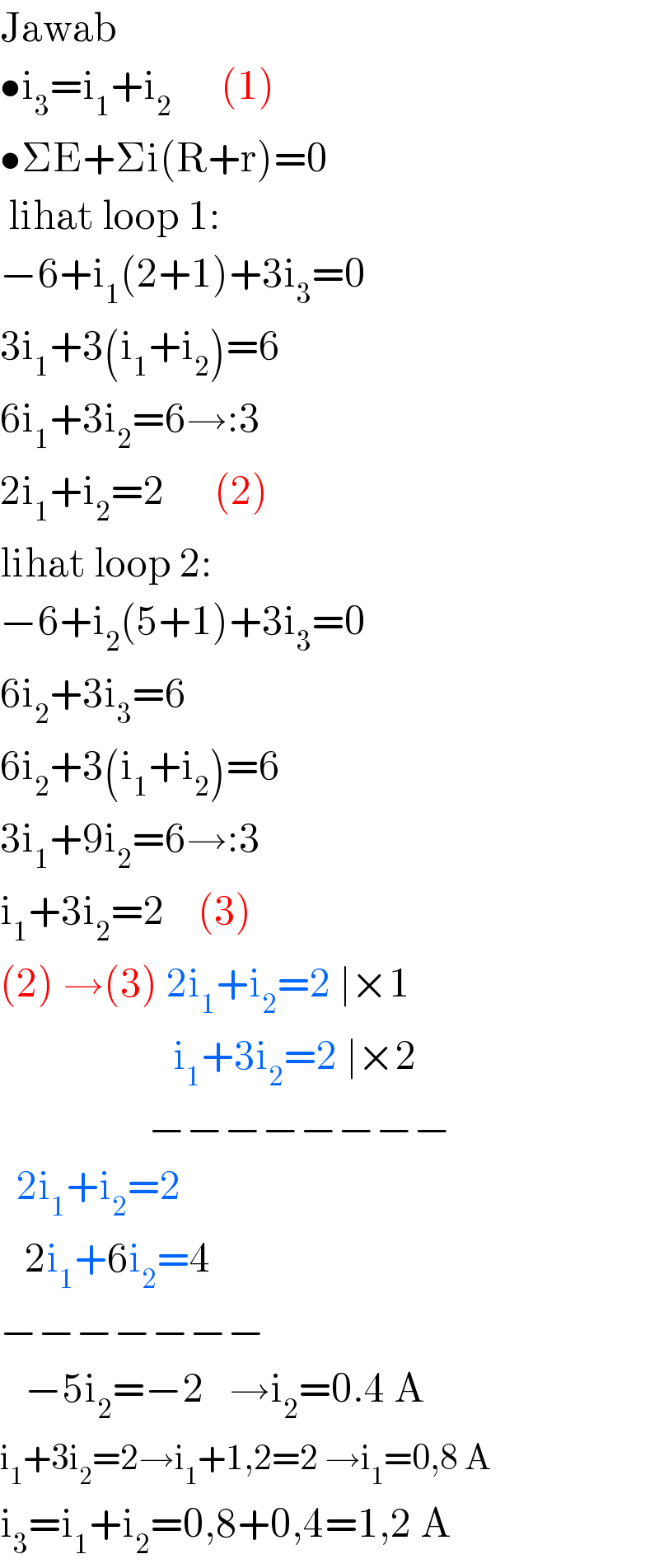
$$\mathrm{Jawab} \\ $$$$\bullet\mathrm{i}_{\mathrm{3}} =\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} \:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\bullet\Sigma\mathrm{E}+\Sigma\mathrm{i}\left(\mathrm{R}+\mathrm{r}\right)=\mathrm{0} \\ $$$$\:\mathrm{lihat}\:\mathrm{loop}\:\mathrm{1}: \\ $$$$−\mathrm{6}+\mathrm{i}_{\mathrm{1}} \left(\mathrm{2}+\mathrm{1}\right)+\mathrm{3i}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{3i}_{\mathrm{1}} +\mathrm{3}\left(\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} \right)=\mathrm{6}\: \\ $$$$\mathrm{6i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{6}\rightarrow:\mathrm{3}\: \\ $$$$\mathrm{2i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{2}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{lihat}\:\mathrm{loop}\:\mathrm{2}: \\ $$$$−\mathrm{6}+\mathrm{i}_{\mathrm{2}} \left(\mathrm{5}+\mathrm{1}\right)+\mathrm{3i}_{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{6i}_{\mathrm{2}} +\mathrm{3i}_{\mathrm{3}} =\mathrm{6} \\ $$$$\mathrm{6i}_{\mathrm{2}} +\mathrm{3}\left(\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} \right)=\mathrm{6} \\ $$$$\mathrm{3i}_{\mathrm{1}} +\mathrm{9i}_{\mathrm{2}} =\mathrm{6}\rightarrow:\mathrm{3} \\ $$$$\mathrm{i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{2}\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right)\:\rightarrow\left(\mathrm{3}\right)\:\mathrm{2i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{2}\:\mid×\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{2}\:\mid×\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−−−−−−− \\ $$$$\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{2} \\ $$$$\:\:\:\mathrm{2i}_{\mathrm{1}} +\mathrm{6i}_{\mathrm{2}} =\mathrm{4} \\ $$$$−−−−−−− \\ $$$$\:\:\:−\mathrm{5i}_{\mathrm{2}} =−\mathrm{2}\:\:\:\rightarrow\mathrm{i}_{\mathrm{2}} =\mathrm{0}.\mathrm{4}\:\mathrm{A} \\ $$$$\mathrm{i}_{\mathrm{1}} +\mathrm{3i}_{\mathrm{2}} =\mathrm{2}\rightarrow\mathrm{i}_{\mathrm{1}} +\mathrm{1},\mathrm{2}=\mathrm{2}\:\rightarrow\mathrm{i}_{\mathrm{1}} =\mathrm{0},\mathrm{8}\:\mathrm{A} \\ $$$$\mathrm{i}_{\mathrm{3}} =\mathrm{i}_{\mathrm{1}} +\mathrm{i}_{\mathrm{2}} =\mathrm{0},\mathrm{8}+\mathrm{0},\mathrm{4}=\mathrm{1},\mathrm{2}\:\mathrm{A} \\ $$
Answered by DELETED last updated on 05/Sep/21
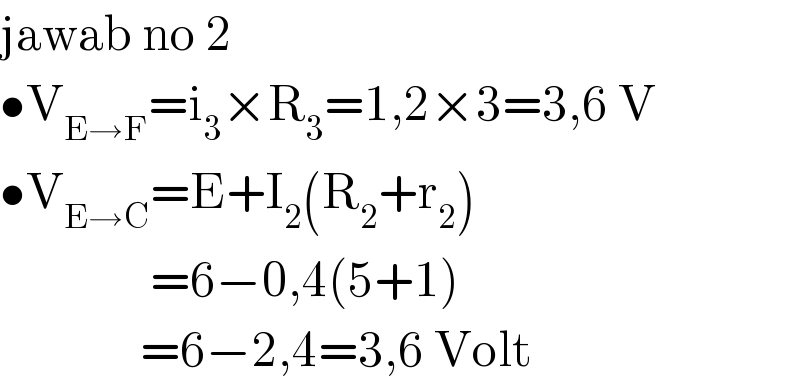
$$\mathrm{jawab}\:\mathrm{no}\:\mathrm{2} \\ $$$$\bullet\mathrm{V}_{\mathrm{E}\rightarrow\mathrm{F}} =\mathrm{i}_{\mathrm{3}} ×\mathrm{R}_{\mathrm{3}} =\mathrm{1},\mathrm{2}×\mathrm{3}=\mathrm{3},\mathrm{6}\:\mathrm{V} \\ $$$$\bullet\mathrm{V}_{\mathrm{E}\rightarrow\mathrm{C}} =\mathrm{E}+\mathrm{I}_{\mathrm{2}} \left(\mathrm{R}_{\mathrm{2}} +\mathrm{r}_{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}−\mathrm{0},\mathrm{4}\left(\mathrm{5}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}−\mathrm{2},\mathrm{4}=\mathrm{3},\mathrm{6}\:\mathrm{Volt} \\ $$
