Menu Close

Question-153203

Tinku Tara 0 Comments
Pin




Question Number 153203 by mathdanisur last updated on 05/Sep/21
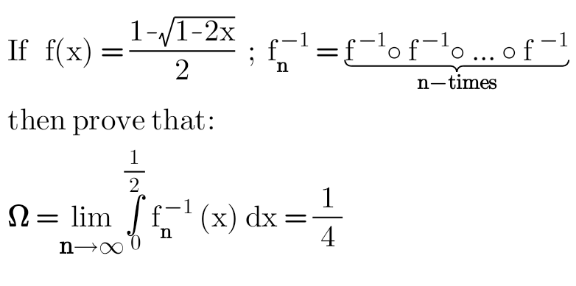
Answered by Kamel last updated on 05/Sep/21
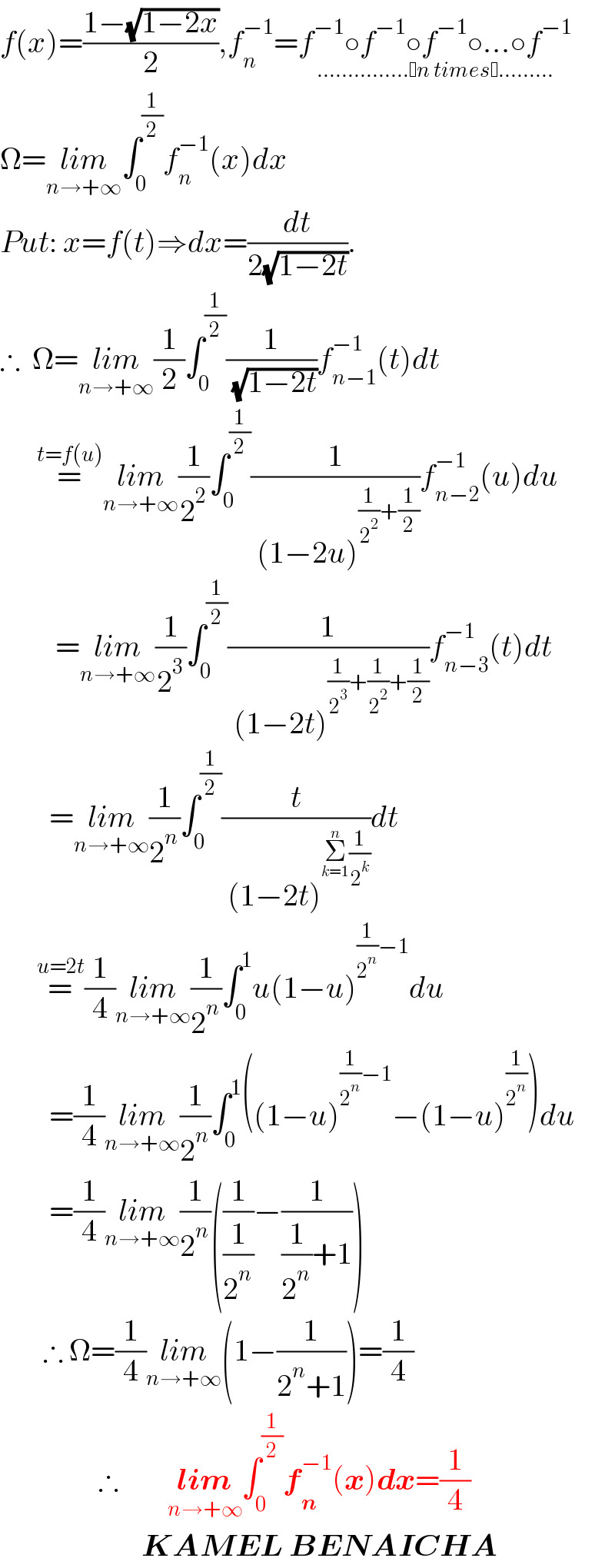
f(x)=((1−(√(1−2x)))/2),f_n ^(−1) =f^(−1) ○f^(−1) ○f^(−1) ○...○f^(−1) _(............... n times .........) Ω=lim_(n→+∞) ∫_0 ^(1/2) f_n ^(−1) (x)dx Put: x=f(t)⇒dx=(dt/(2(√(1−2t)))). ∴ Ω=lim_(n→+∞) (1/2)∫_0 ^(1/2) (1/( (√(1−2t))))f_(n−1) ^(−1) (t)dt =^(t=f(u)) lim_(n→+∞) (1/2^2 )∫_0 ^(1/2) (1/( (1−2u)^((1/2^2 )+(1/2)) ))f_(n−2) ^(−1) (u)du =lim_(n→+∞) (1/2^3 )∫_0 ^(1/2) (1/( (1−2t)^((1/2^3 )+(1/2^2 )+(1/2)) ))f_(n−3) ^(−1) (t)dt =lim_(n→+∞) (1/2^n )∫_0 ^(1/2) (t/( (1−2t)^(Σ_(k=1) ^n (1/2^k )) ))dt =^(u=2t) (1/4)lim_(n→+∞) (1/2^n )∫_0 ^1 u(1−u)^((1/2^n )−1) du =(1/4)lim_(n→+∞) (1/2^n )∫_0 ^1 ((1−u)^((1/2^n )−1) −(1−u)^(1/2^n ) )du =(1/4)lim_(n→+∞) (1/2^n )((1/(1/2^n ))−(1/((1/2^n )+1))) ∴ Ω=(1/4)lim_(n→+∞) (1−(1/(2^n +1)))=(1/4) ∴ lim_(n→+∞) ∫_0 ^(1/2) f_n ^(−1) (x)dx=(1/4) KAMEL BENAICHA
$${f}\left({x}\right)=\frac{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{2}{x}}}{\mathrm{2}},{f}_{{n}} ^{−\mathrm{1}} =\underset{…………… {n}\:{times} ………} {{f}^{−\mathrm{1}} \circ{f}^{−\mathrm{1}} \circ{f}^{−\mathrm{1}} \circ…\circ{f}^{−\mathrm{1}} } \\ $$$$\Omega=\underset{{n}\rightarrow+\infty} {{lim}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {f}_{{n}} ^{−\mathrm{1}} \left({x}\right){dx} \\ $$$${Put}:\:{x}={f}\left({t}\right)\Rightarrow{dx}=\frac{{dt}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{2}{t}}}. \\ $$$$\therefore\:\:\Omega=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{2}{t}}}{f}_{{n}−\mathrm{1}} ^{−\mathrm{1}} \left({t}\right){dt} \\ $$$$\:\:\:\:\:\:\overset{{t}={f}\left({u}\right)} {=}\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\:\left(\mathrm{1}−\mathrm{2}{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}} }{f}_{{n}−\mathrm{2}} ^{−\mathrm{1}} \left({u}\right){du} \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{1}}{\:\left(\mathrm{1}−\mathrm{2}{t}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}} }{f}_{{n}−\mathrm{3}} ^{−\mathrm{1}} \left({t}\right){dt} \\ $$$$\:\:\:\:\:\:\:\:=\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{t}}{\:\left(\mathrm{1}−\mathrm{2}{t}\right)^{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }} }{dt} \\ $$$$\:\:\:\:\:\:\overset{{u}=\mathrm{2}{t}} {=}\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int_{\mathrm{0}} ^{\mathrm{1}} {u}\left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }−\mathrm{1}} {du} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\int_{\mathrm{0}} ^{\mathrm{1}} \left(\left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }−\mathrm{1}} −\left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} \right){du} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\rightarrow+\infty} {{lim}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }}−\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\therefore\:\Omega=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}\rightarrow+\infty} {{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\:\:\underset{{n}\rightarrow+\infty} {\boldsymbol{{lim}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{f}}_{\boldsymbol{{n}}} ^{−\mathrm{1}} \left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{KAMEL}}\:\boldsymbol{{BENAICHA}} \\ $$
Answered by liberty last updated on 05/Sep/21
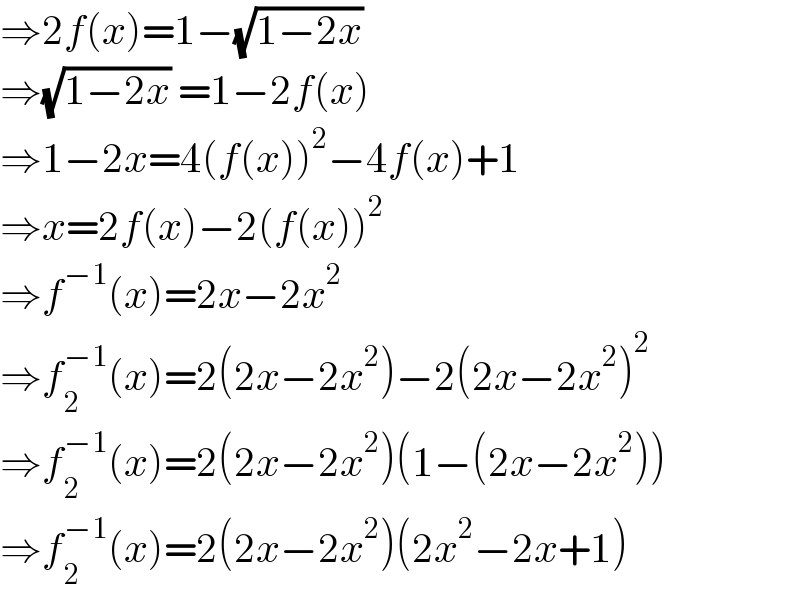
⇒2f(x)=1−(√(1−2x)) ⇒(√(1−2x)) =1−2f(x) ⇒1−2x=4(f(x))^2 −4f(x)+1 ⇒x=2f(x)−2(f(x))^2 ⇒f^(−1) (x)=2x−2x^2 ⇒f_2 ^(−1) (x)=2(2x−2x^2 )−2(2x−2x^2 )^2 ⇒f_2 ^(−1) (x)=2(2x−2x^2 )(1−(2x−2x^2 )) ⇒f_2 ^(−1) (x)=2(2x−2x^2 )(2x^2 −2x+1)
$$\Rightarrow\mathrm{2}{f}\left({x}\right)=\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{2}{x}} \\ $$$$\Rightarrow\sqrt{\mathrm{1}−\mathrm{2}{x}}\:=\mathrm{1}−\mathrm{2}{f}\left({x}\right) \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}{x}=\mathrm{4}\left({f}\left({x}\right)\right)^{\mathrm{2}} −\mathrm{4}{f}\left({x}\right)+\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{2}{f}\left({x}\right)−\mathrm{2}\left({f}\left({x}\right)\right)^{\mathrm{2}} \\ $$$$\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \\ $$$$\Rightarrow{f}_{\mathrm{2}} ^{−\mathrm{1}} \left({x}\right)=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow{f}_{\mathrm{2}} ^{−\mathrm{1}} \left({x}\right)=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\right) \\ $$$$\Rightarrow{f}_{\mathrm{2}} ^{−\mathrm{1}} \left({x}\right)=\mathrm{2}\left(\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *