Menu Close

Question-15322

Tinku Tara 0 Comments
Pin




Question Number 15322 by tawa tawa last updated on 09/Jun/17
Commented by mrW1 last updated on 09/Jun/17
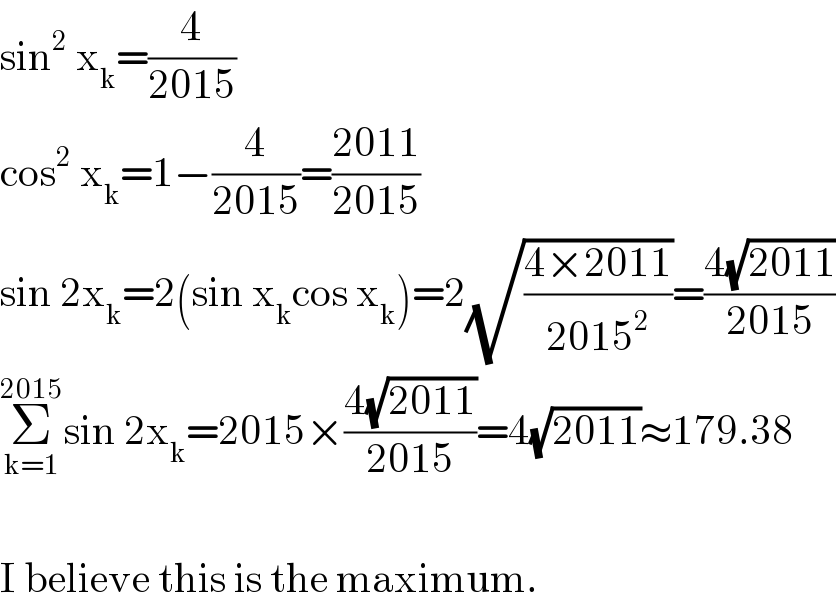
sin^2 x_k =(4/(2015)) cos^2 x_k =1−(4/(2015))=((2011)/(2015)) sin 2x_k =2(sin x_k cos x_k )=2(√((4×2011)/(2015^2 )))=((4(√(2011)))/(2015)) Σ_(k=1) ^(2015) sin 2x_k =2015×((4(√(2011)))/(2015))=4(√(2011))≈179.38 I believe this is the maximum.
$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}_{\mathrm{k}} =\frac{\mathrm{4}}{\mathrm{2015}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}_{\mathrm{k}} =\mathrm{1}−\frac{\mathrm{4}}{\mathrm{2015}}=\frac{\mathrm{2011}}{\mathrm{2015}} \\ $$$$\mathrm{sin}\:\mathrm{2x}_{\mathrm{k}} =\mathrm{2}\left(\mathrm{sin}\:\mathrm{x}_{\mathrm{k}} \mathrm{cos}\:\mathrm{x}_{\mathrm{k}} \right)=\mathrm{2}\sqrt{\frac{\mathrm{4}×\mathrm{2011}}{\mathrm{2015}^{\mathrm{2}} }}=\frac{\mathrm{4}\sqrt{\mathrm{2011}}}{\mathrm{2015}} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\mathrm{sin}\:\mathrm{2x}_{\mathrm{k}} =\mathrm{2015}×\frac{\mathrm{4}\sqrt{\mathrm{2011}}}{\mathrm{2015}}=\mathrm{4}\sqrt{\mathrm{2011}}\approx\mathrm{179}.\mathrm{38} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{believe}\:\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{maximum}. \\ $$
Commented by tawa tawa last updated on 09/Jun/17
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 09/Jun/17
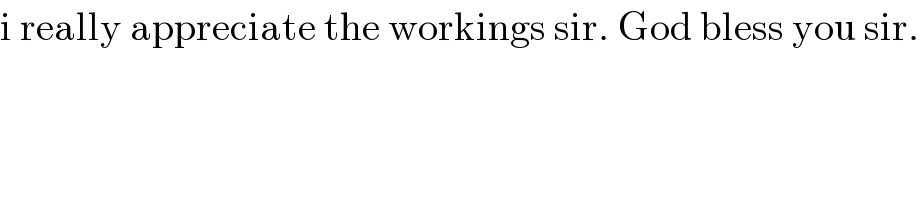
i really appreciate the workings sir. God bless you sir.
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{the}\:\mathrm{workings}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 09/Jun/17
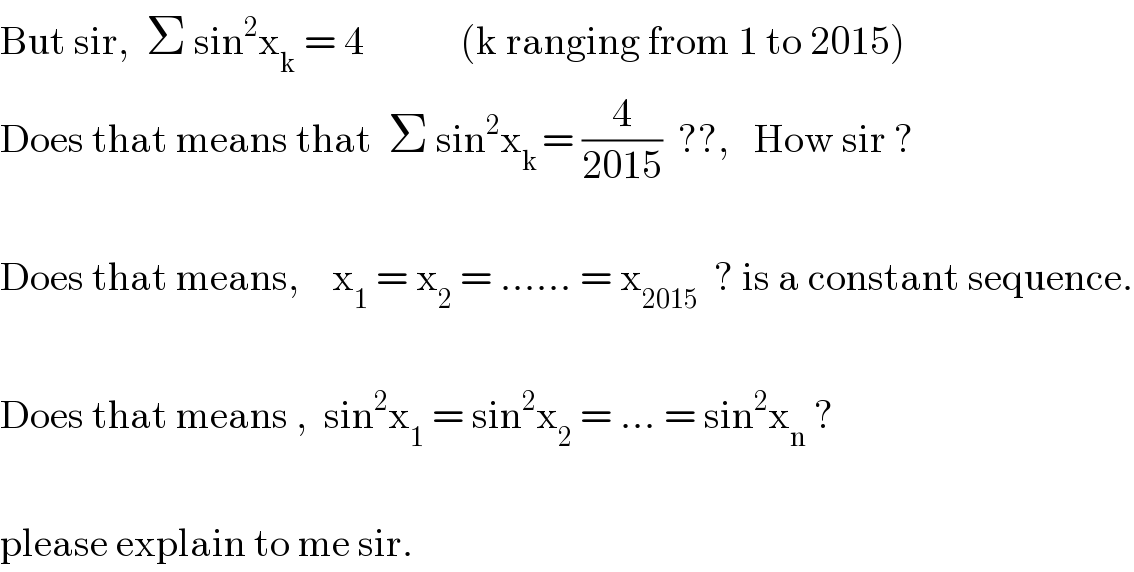
But sir, Σ sin^2 x_k = 4 (k ranging from 1 to 2015) Does that means that Σ sin^2 x_(k ) = (4/(2015)) ??, How sir ? Does that means, x_1 = x_2 = ...... = x_(2015) ? is a constant sequence. Does that means , sin^2 x_1 = sin^2 x_2 = ... = sin^2 x_n ? please explain to me sir.
$$\mathrm{But}\:\mathrm{sir},\:\:\Sigma\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}_{\mathrm{k}} \:=\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{k}\:\mathrm{ranging}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{2015}\right) \\ $$$$\mathrm{Does}\:\mathrm{that}\:\mathrm{means}\:\mathrm{that}\:\:\Sigma\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}_{\mathrm{k}\:} =\:\frac{\mathrm{4}}{\mathrm{2015}}\:\:??,\:\:\:\mathrm{How}\:\mathrm{sir}\:? \\ $$$$ \\ $$$$\mathrm{Does}\:\mathrm{that}\:\mathrm{means},\:\:\:\:\mathrm{x}_{\mathrm{1}} \:=\:\mathrm{x}_{\mathrm{2}} \:=\:……\:=\:\mathrm{x}_{\mathrm{2015}} \:\:?\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{sequence}. \\ $$$$ \\ $$$$\mathrm{Does}\:\mathrm{that}\:\mathrm{means}\:,\:\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}_{\mathrm{1}} \:=\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}_{\mathrm{2}} \:=\:…\:=\:\mathrm{sin}^{\mathrm{2}} \mathrm{x}_{\mathrm{n}} \:? \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{explain}\:\mathrm{to}\:\mathrm{me}\:\mathrm{sir}.\: \\ $$
Commented by mrW1 last updated on 09/Jun/17
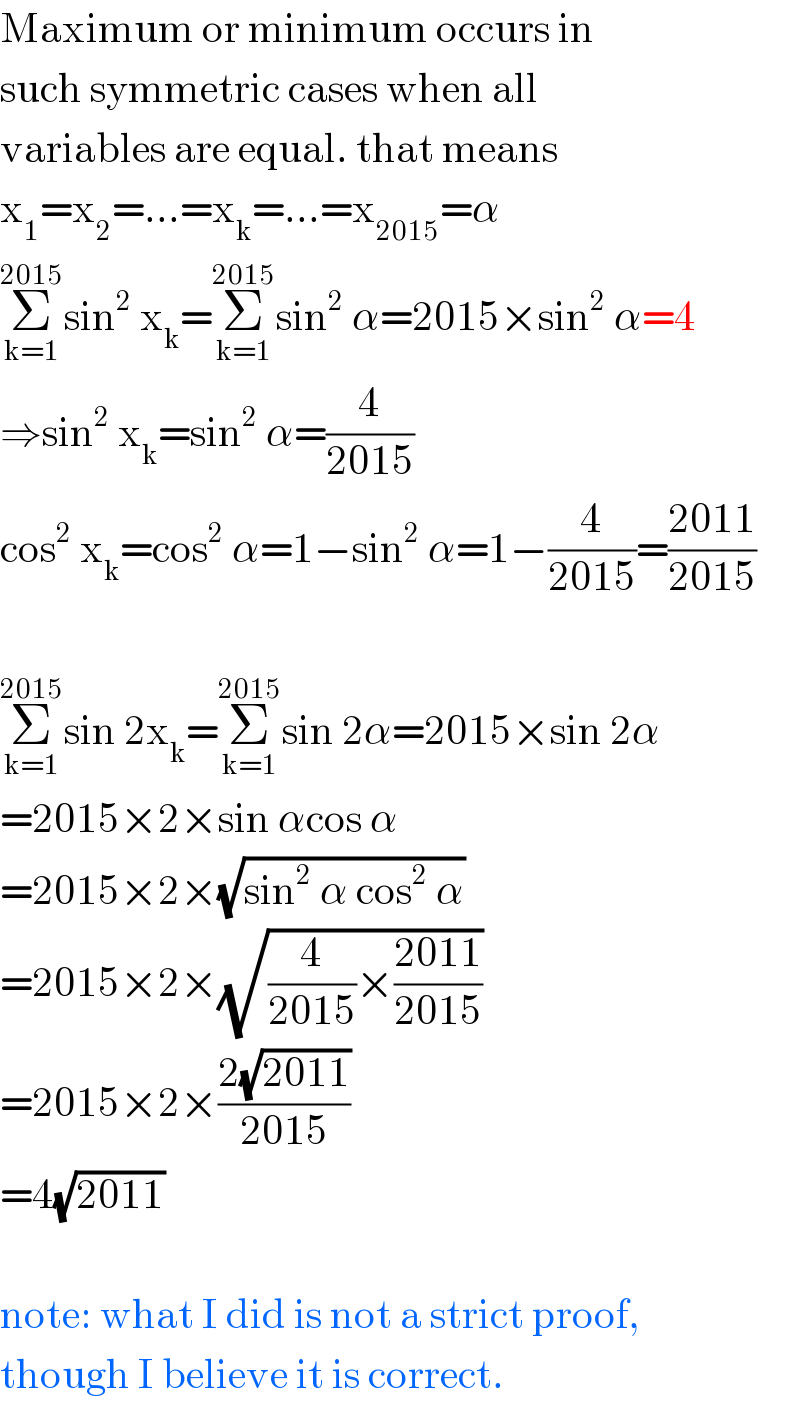
Maximum or minimum occurs in such symmetric cases when all variables are equal. that means x_1 =x_2 =...=x_k =...=x_(2015) =α Σ_(k=1) ^(2015) sin^2 x_k =Σ_(k=1) ^(2015) sin^2 α=2015×sin^2 α=4 ⇒sin^2 x_k =sin^2 α=(4/(2015)) cos^2 x_k =cos^2 α=1−sin^2 α=1−(4/(2015))=((2011)/(2015)) Σ_(k=1) ^(2015) sin 2x_k =Σ_(k=1) ^(2015) sin 2α=2015×sin 2α =2015×2×sin αcos α =2015×2×(√(sin^2 α cos^2 α)) =2015×2×(√((4/(2015))×((2011)/(2015)))) =2015×2×((2(√(2011)))/(2015)) =4(√(2011)) note: what I did is not a strict proof, though I believe it is correct.
$$\mathrm{Maximum}\:\mathrm{or}\:\mathrm{minimum}\:\mathrm{occurs}\:\mathrm{in} \\ $$$$\mathrm{such}\:\mathrm{symmetric}\:\mathrm{cases}\:\mathrm{when}\:\mathrm{all} \\ $$$$\mathrm{variables}\:\mathrm{are}\:\mathrm{equal}.\:\mathrm{that}\:\mathrm{means} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{2}} =…=\mathrm{x}_{\mathrm{k}} =…=\mathrm{x}_{\mathrm{2015}} =\alpha \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}_{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{2015}×\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{4} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}_{\mathrm{k}} =\mathrm{sin}^{\mathrm{2}} \:\alpha=\frac{\mathrm{4}}{\mathrm{2015}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\mathrm{x}_{\mathrm{k}} =\mathrm{cos}^{\mathrm{2}} \:\alpha=\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\alpha=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{2015}}=\frac{\mathrm{2011}}{\mathrm{2015}} \\ $$$$ \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\mathrm{sin}\:\mathrm{2x}_{\mathrm{k}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2015}} {\sum}}\mathrm{sin}\:\mathrm{2}\alpha=\mathrm{2015}×\mathrm{sin}\:\mathrm{2}\alpha \\ $$$$=\mathrm{2015}×\mathrm{2}×\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha \\ $$$$=\mathrm{2015}×\mathrm{2}×\sqrt{\mathrm{sin}^{\mathrm{2}} \:\alpha\:\mathrm{cos}^{\mathrm{2}} \:\alpha} \\ $$$$=\mathrm{2015}×\mathrm{2}×\sqrt{\frac{\mathrm{4}}{\mathrm{2015}}×\frac{\mathrm{2011}}{\mathrm{2015}}} \\ $$$$=\mathrm{2015}×\mathrm{2}×\frac{\mathrm{2}\sqrt{\mathrm{2011}}}{\mathrm{2015}} \\ $$$$=\mathrm{4}\sqrt{\mathrm{2011}} \\ $$$$ \\ $$$$\mathrm{note}:\:\mathrm{what}\:\mathrm{I}\:\mathrm{did}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{strict}\:\mathrm{proof}, \\ $$$$\mathrm{though}\:\mathrm{I}\:\mathrm{believe}\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}. \\ $$
Commented by tawa tawa last updated on 09/Jun/17
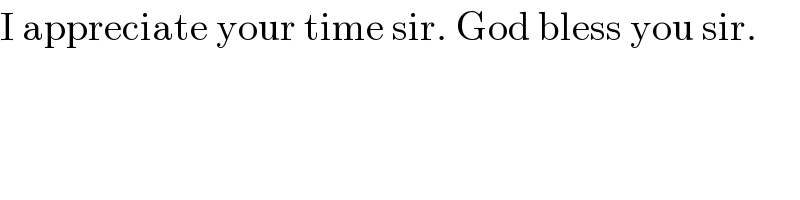
I appreciate your time sir. God bless you sir.
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *