Question Number 153239 by rexford last updated on 06/Sep/21
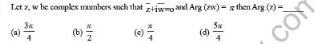
Answered by MJS_new last updated on 06/Sep/21
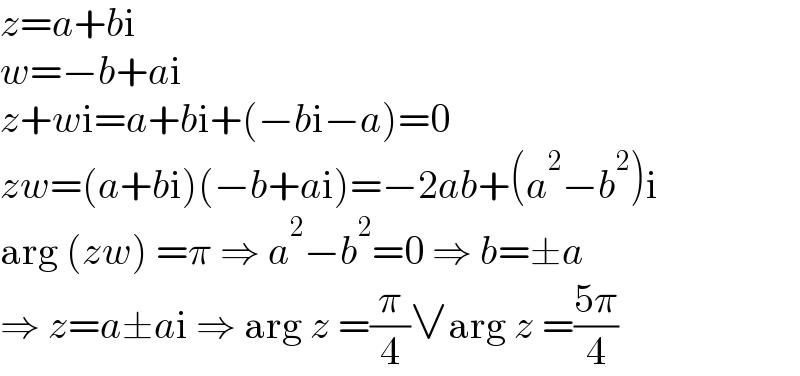
$${z}={a}+{b}\mathrm{i} \\ $$$${w}=−{b}+{a}\mathrm{i} \\ $$$${z}+{w}\mathrm{i}={a}+{b}\mathrm{i}+\left(−{b}\mathrm{i}−{a}\right)=\mathrm{0} \\ $$$${zw}=\left({a}+{b}\mathrm{i}\right)\left(−{b}+{a}\mathrm{i}\right)=−\mathrm{2}{ab}+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{i} \\ $$$$\mathrm{arg}\:\left({zw}\right)\:=\pi\:\Rightarrow\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{b}=\pm{a} \\ $$$$\Rightarrow\:{z}={a}\pm{a}\mathrm{i}\:\Rightarrow\:\mathrm{arg}\:{z}\:=\frac{\pi}{\mathrm{4}}\vee\mathrm{arg}\:{z}\:=\frac{\mathrm{5}\pi}{\mathrm{4}} \\ $$
